2015-07-21
283
Во многих случаях интересующее нас событие 
может произойти только вместе с одним из событий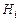 
, 
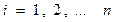. Например, рассмотрим такой опыт. В холле МИЭТ остановили случайно встреченного студента, проверили, знает ли он аксиомы теории вероятностей. Событие 
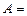{выбранный студент знает аксиомы} может произойти только вместе с одним из событий 
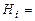{выбранный студент учится на 
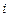-м курсе}, 
.
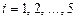Отметим, что множество событий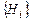 
в этом и подобных случаях обладает такими свойствами:
а) в каждом опыте (например, по случайному выбору студента) обязательно происходит какое-либо из событий 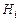, т.е.
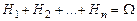
(в этом случае говорят, что 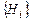- полная группа событий);
б) события 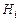попарно несовместны:
.
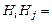
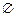Итак, пусть в случайном опыте событие может произойти только вместе с одним из событий ,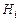 
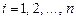, образующих полную группу попарно несовместных событий ( 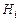называют гипотезами). Тогда справедливо равенство
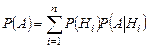(1.9.1)
(формула полной вероятности).
◄Представим в виде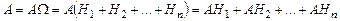 
, см. рис. 1.9.1. Поскольку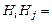 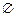, то и события 
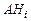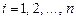, попарно несовместны, поэтому с учётом аксиомы сложения имеем:
|
|
|
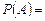
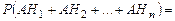
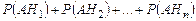. (1.9.2)
 |
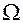
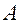
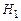
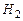
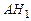
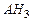
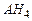
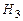
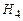
Рис. 1.9.1. К доказательству формулы полной вероятности
Далее, используя формулу умножения вероятностей (1.7.4), запишем: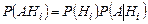 
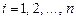, , откуда с учётом (1.9.2) получаем (1.9.1).►
