2015-07-21
429
На трёх заводах производятся однотипные изделия. В магазин поступило 50 изделий с первого завода, 20 изделий – со второго завода и 30 изделий –с третьего завода. Брак в общем количестве изделий, производимых на первом заводе, составляет 1%, на втором заводе – 2% и на третьем заводе – 3%. В магазине наудачу выбрано одно изделие для покупки. С какой вероятностью это изделие является бракованным?
◄Введём обозначения: 
={выбрано бракованное изделие},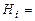 
{выбранное изделие изготовлено на 
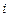-ом заводе}, 
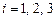. Очевидно, гипотезы 
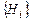- составляют полную группу попарно несовместных событий.
Согласно условию задачи, вероятности гипотез равны: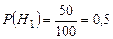 
, 
, 
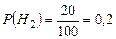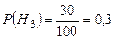, а условные вероятности события равны: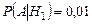 
, 
, 
.
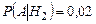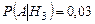По формуле полной вероятности (1.9.1) находим: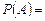 
.►
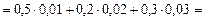
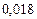Замечания
1. В примере 1.9.1 формулу полной вероятности можно интерпретировать следующим образом: вероятность брака в магазине равна взвешенной сумме вероятностей брака на заводах с весами, равными долям, которые составляют поставки заводов в общем количестве изделий в магазине.
2. Формула (1.9.1) справедлива, если введённые в рассмотрение гипотезы 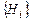образуют полную группу попарно несовместных событий. Поэтому при решении задач желательно убеждаться, в том, что 
.
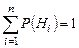Однако в некоторых случаях полная группа гипотез может содержать большое число событий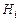 
, при этом для многих из них оказывается, что 
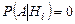, т.е. вклада в правую часть формулы (1.9.1) такие гипотезы 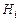не вносят. В таких случаях целесообразно сократить число рассматриваемых гипотез, оставив только те из них, для которых 
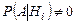. При этом, хотя множество гипотез 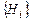и не будет полной группой, формула полной вероятности даст верный результат.
