Четыре артиллерийских расчёта производят по одному выстрелу по одной и той же цели. Вероятность попадания для 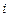 -го расчёта равна
-го расчёта равна 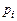 ,
, 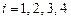 . При менее, чем трёх попаданиях цель поражена не будет. При трёх попаданиях цель будет уничтожена с вероятностью
. При менее, чем трёх попаданиях цель поражена не будет. При трёх попаданиях цель будет уничтожена с вероятностью 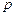 , а при четырёх попаданиях – с полной достоверностью. Найти вероятность того, что цель будет уничтожена (событие
, а при четырёх попаданиях – с полной достоверностью. Найти вероятность того, что цель будет уничтожена (событие  ).
).
◄Полная группа гипотез в данном случае совпадает с пространством элементарных исходов. Перечислим гипотезы, обозначив их 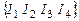 , где
, где 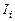 - индикатор попадания для
- индикатор попадания для 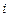 -го расчёта, т.е.
-го расчёта, т.е. 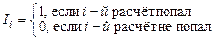 :
:
{0 0 0 0}
{1 0 0 0}, {0 1 0 0}, {0 0 1 0}, {0 0 0 1}
{1 1 0 0}, {1 0 1 0}, {1 0 0 1}, {0 1 1 0}, {0 1 0 1}, {0 0 1 1}
{1 1 1 0}, {1 1 0 1}, {1 0 1 1}, {0 1 1 1}
{1 1 1 1}
Итак, полная группа гипотез состоит из 16 событий. Но свойством 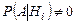 обладают только 5 из них, поэтому вводим в рассмотрение только такие гипотезы:
обладают только 5 из них, поэтому вводим в рассмотрение только такие гипотезы: 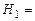 {1 1 1 0},
{1 1 1 0}, 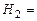 {1 1 0 1},
{1 1 0 1}, 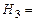 {1 0 1 1},
{1 0 1 1}, 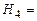 {0 1 1 1},
{0 1 1 1}, 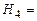 {1 1 1 1}.
{1 1 1 1}.
Далее, находим:
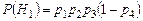 ,
, 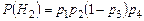 ,
, 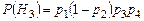 ,
, 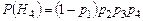 ,
, 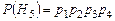 ;
;
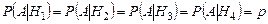 ,
, 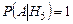 .
.
Окончательно, по формуле (3.3.1) получаем:
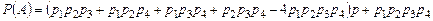 .►
.►
Упражнения
1.9.1. В одной урне – 1 белый и 3 чёрных шара, во второй – 2 белых и 2 чёрных шара. Наудачу выбирают урну, из которой наудачу вынимают шар. С какой вероятностью этот шар белый?
1.9.2. В первой урне были: 1 белый и 3 чёрных шара, во второй – 2 белых и 2 чёрных шара. Из первой урны наудачу вынули шар и переложили его во вторую урну, после чего из второй урны извлекли наудачу один шар. С какой вероятностью этот шар белый?
1.9.3. Проверяется партия приборов, среди которых 10% дефектных. Проверка с вероятностью 0,95 позволяет обнаружить дефект, если он есть. Если же дефекта нет, то с вероятностью 0,03 прибор ошибочно признаётся неисправным. С какой вероятностью проверяемый прибор будет признан дефектным?
Ответы к упражнениям
1.9.1. 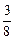 .
.
1.9.2. 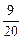 .
.
1.9.3. 0,122.
 2015-07-21
2015-07-21 305
305








