2015-07-14
372
Определение Касательной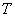 
к графику функции 
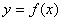называется предельное положение секущей при стремлении точки 
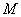к точке 
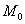вдоль графика(при этом 
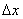стремится нулю). Предположим, что кривая 
имеет в точке 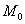касательную. Очевидно, 
.
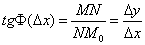Имеем право перейти к пределу при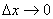 
,т.к. предположили, что кривая имеет касательную 
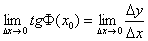или, в силу непрерывности функции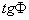 
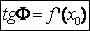
Таким образом, производная функции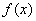 
в точке 
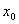равна угловому коэффициенту касательной 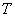проведённой к графику функции 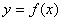в точке 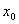. Запишем уравнение касательной 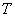. Как известно из аналитической геометрии, уравнение прямой с угловым коэффициентом k через точку 
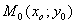имеет вид 
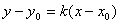для касательной 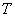будем, следовательно, иметь уравнение (T) 
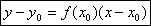В частности, если 
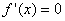то касательная имеет уравнение 
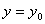, т.е. горизонталь. Заметим, что если производная функции 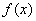в точке 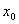бесконечная, то касательная к её графику в точке М вертикальна и имеет уравнение 
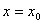. Нормалью к графику функции 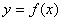в точке х0 называется прямая, проходящая через эту точку перпендикулярно касательной (Т). Следовательно, уравнение касательной имеет вид: 
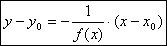- уравнение нормали (N)
