Теорема

Для того чтобы функция f(x), была дифференцируема в точке х₀ необходимо и достаточно, чтобы она имела в этой точке конечную производную. Док-во: Пусть функция f(x) дифференцируема в точке x₀, тогда имеет место равенство (4). Считая 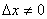, из (4) получим: 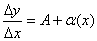переходим к пределу при 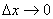: 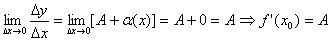, т.е. в точке х₀ существует конечная производная. Обратно Пусть в точке х₀ функция имеет конечную производную 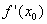. Обозначим её А, она равняется: 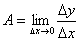, - откуда 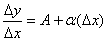, где 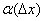- БМ при 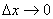. Умножая обе части на 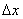последнее уравнение, приходим к уравнению (4), т.е. f(x) в точке х₀ дифференцируема. q.e.d. Таким образом, дифференцируемость функции в точке и существование в этой точке её конечной производной - понятия равносильные (для функции многих переменных это будет не так).