Аналитическая геометрия на плоскости

Первая задача аналитической геометрии – представление геометрической фигуры уравнением или неравенством, системой уравнений или неравенств на основе применения координат. Вторая задача аналитической геометрии – исследовать, какие геометрические фигуры представляются теми или иными уравнениями.

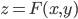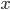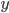Пусть – функция двух вещественных переменных и . Уравнение 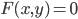задает линию или кривую, если

1. координаты каждой точки линии удовлетворяют этому уравнению и

2. координаты точки, не принадлежащей линии, не удовлетворяют

этому уравнению.

При этом уравнение может задавать точку, отрезок или пустое множество. Уравнение называется алгебраическим степени 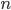, если его левая часть представляет собой многочлен степени 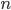относительно 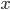и 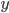с численными коэффициентами.

Линейное программирование — математическая дисциплина, посвящённая теории и методам решения экстремальных задач на множествах 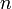-мерного векторного пространства, задаваемых системами линейных уравнений и неравенств.

Линейное программирование является частным случаем выпуклого программирования, которое в свою очередь является частным случаем математического программирования. Одновременно оно — основа нескольких методов решения задач целочисленного и нелинейного программирования. Одним из обобщений линейного программирования является дробно-линейное программирование.

Многие свойства задач линейного программирования можно интерпретировать также как свойства многогранников и таким образом геометрически формулировать и доказывать их.