Представление синусоидальных токов и напряжений вращающимися векторами на комплексной плоскости и в комплексной форме. Векторные диаграммы токов и напряжений

Из курса математики известно, что любую синусоидальную функцию времени, на­пример i (t) = Im ∙sin(wt+a), можно изобразить вращающимся векто­ром при соблюдении следую­щих условий:

а) длина вектора в масштабе равна амплитуде функции Im;

y

б) начальное положение вектора при t = 0 определяется начальной фа­зой a;

i (t ¢)

w

Рис. 37

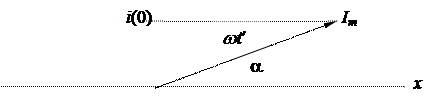в) вектор равномерно вращается с угловой скоростью w, равной угло­вой частоте функции.

При соблюдении названных условий проекция вращающегося вектора на вертикаль­ную ось y в системе координат х-у в любой момент времени t ¢равна мгновенному значению функции i (t ¢), следовательно, i = Im∙ sin(wt+a)

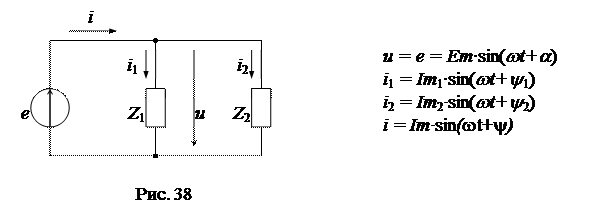
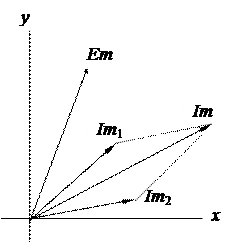
Рассмотрим процессы в схеме электрической цепи рис. 36. Изобразим си­нусоидаль­ные функции токов и напряжений вращающимися векторами для произвольного момента времени, например t = 0 (рис. 37а). При рассмотрении установившегося режима в схеме мгно­венные значения функций не представ­ляют интереса, поэтому момент времени, для которого строится векторная диа­грамма, может быть выбран произвольно. Целесообразно один из век­торов при­нять начальным или исходным и совместить его на диаграмме с одной из осей ко­ординат (вектор Е на рис. 37б совмещен с осью y), при этом остальные век­торы располагают по отношению к исходному вектору под углами, равными их сдвигам фаз.

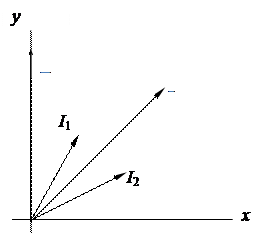
Так как на практике интерес представляют действующие значения токов и напряже­ний, то на векторных диаграммах длины векторов принимают рав­ными в выбранных мас­штабах их действующим значениям (рис. 39б).

Рис. 39

б)

а)

Совокупность векторов токов и напряжений, характеризующих про­цессы в цепи перемен­ного тока, по­строенных в выбранных масштабах и с со­блюдением правильной их ориентации друг отно­сительно друга, называется векторной диаграммой.

6. Переменный ток в идеальном резисторе R. Сопротивление идеального резистора в комплексной форме.

Пусть к цепи с резистором R (рис. 43а) приложено переменное напряже­ние:

.

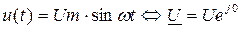Ток и напряжение на зажимах резистора связаны между собой физиче­ским законом Ома, т. е.

,

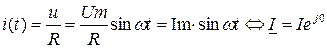Где 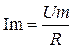, 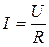- уравнения закона Ома для амплитудных и действующих значений функций.

Угол сдвига фаз между напряжением и током 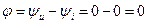, следова­тельно, в цепи с резистором R ток и напряжение совпадают по фазе.

Комплексное сопротивление резистора является чисто вещественным:

.

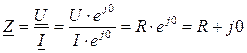Мгновенная мощность в цепи с резистором R всегда положительна:

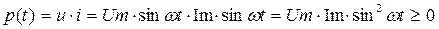
Это означает, что в цепи с резистором R протекает только процесс преоб­разования электрической энергии в другие виды (активный процесс). По этой причине со­противление резистора R на переменном токе называется активным.

Графические диаграммы функций времени u (t), i (t), p (t)представлены на рис. 44, а век­торная диаграмма напряжения и тока - на рис. 43б.

Рис. 44

7. Переменный ток в идеальной катушке с индуктивностью L. Сопротивление идеальной катушки в комплексной форме.

Пусть к цепи с идеальной катушкой L (рис. 45а) приложено переменное напряжение: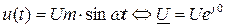

Ток и напряжение на зажимах катушки связаны между собой физиче­ским законом электромагнитной индукции 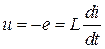, откуда следует:

,

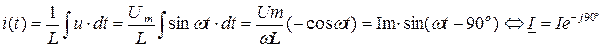где 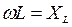- индуктивное реактивное сопротивление катушки,

Уравне­ния закона Ома для амплитудных и действующих значений функ­ций: .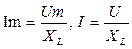

Угол сдвига фаз 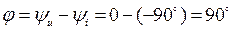, т.е. в цепи с катушкой L ток отстает от напряжения (напряжение опережает ток) на угол .

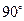Комплексное сопротивление катушки является чисто мнимым и поло­жи­тельным: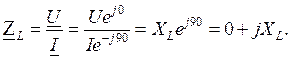

Мгновенная мощность цепи изменяется по синусоидальному закону с частотой 2 w:

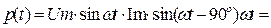
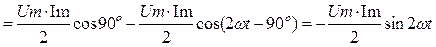
Это означает, что в цепи с катушкой L происходит только периодиче­ский процесс обмена энергией между магнитным полем катушки и источ­ником (реактивный процесс). По этой причине сопротивление катушки пере­менному току X_L =wL называется ре­активным.

Графические диаграммы функций времени u (t), i (t), p (t) представлены на рис. 46, а век­торная диаграмма напряжения и тока - на рис. 45б.

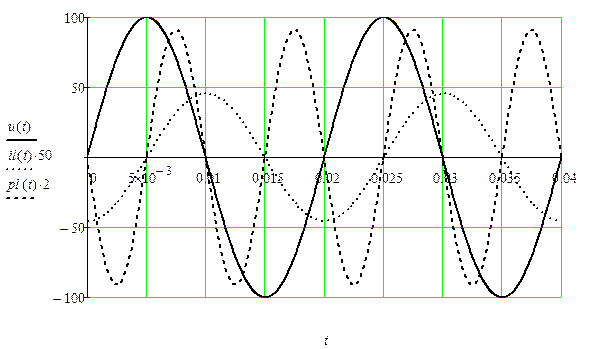Рис. 46

8. Переменный ток в идеальном конденсаторе с емкостью C. Сопротивление идеального конденсатора в комплексной форме.

Пусть к цепи с идеальным конденсатором С (рис. 47а) приложено пере­менное напря­жение

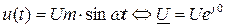
Ток и напряжение на зажимах конденсатора связаны между собой физи­ческим зако­ном сохранения заряда:

,

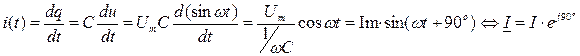где 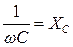- емкостное реактивное сопротивление [Ом].

Уравнения за­кона Ома для амплитудных и действующих значений функций: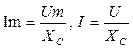

Угол сдвига фаз 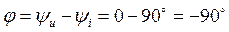, т. е. в цепи с конденсато­ром С ток опе­режает напряжение (напряжение отстает от тока) на угол 90°.

Комплексное сопротивление конденсатора является чисто мнимым и от­рицательным: .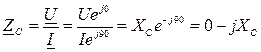

Мгновенная мощность цепи изменяется по синусоидальному закону с частотой 2 w:

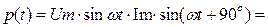
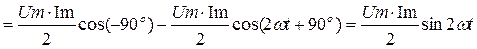
Это означает, что в цепи с конденсатором С происходит только периоди­ческий про­цесс обмена энергией между электрическим полем конденсатора 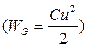и источником (реактивный процесс). По этой причине сопротивле­ние конденсатора переменному току 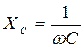называется реактивным.

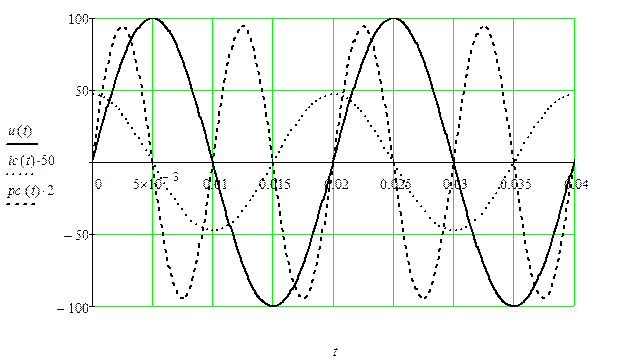Рис. 48