Треугольники напряжений, токов, сопротивлений, проводимостей, мощностей для приемников переменного тока

При расчете электрических цепей переменного тока реальные элементы цепи (при­емники, источники) заменяются эквивалентными схемами замещения, состоящими из ком­бинации идеальных схемных элементов R, L и С.

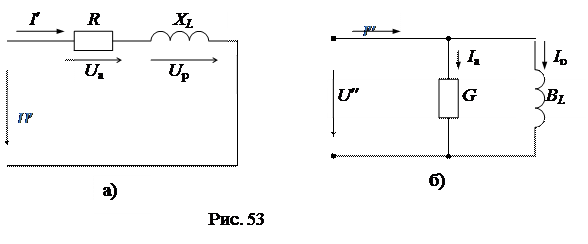
Пусть некоторый приемник энергии носит в целом активно-индуктив­ный характер (например, электродвигатель). Такой приемник может быть пред­став­лен двумя простей­шими схемами замещения, состоящими из 2-х схемных эле­ментов R и L: а) последовательной (рис. 53а) и б) параллельной (рис. 53б):

Обе схемы будут эквивалентны друг другу при условии равенства пара­метров ре­жима на входе: , .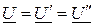

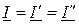Для последовательной схемы (рис. 53а) справедливы соотношения:

,

.

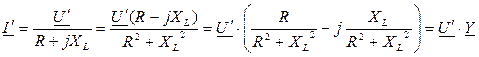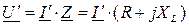Для параллельной схемы (рис. 53б) справедливы соотношения:

,

.

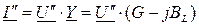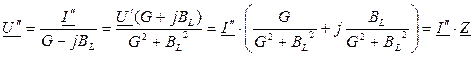Сравнивая правые части уравнений для U и I, получим соотношения между пара­метрами эквивалентных схем:

, , , .

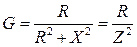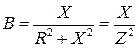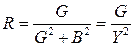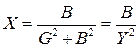Из анализа полученных уравнений следует сделать вывод, что в общем случае 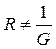и 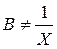и соответственно 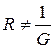и 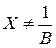, как это имеет место для цепей постоян­ного тока.

Математически любой вектор можно представить состоящим из суммы нескольких векторов или составляющих.

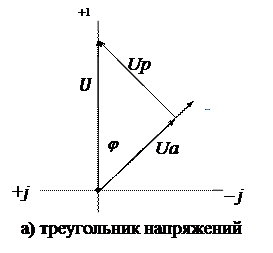
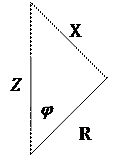
Последовательной схеме замещения соответствует представление век­тора напряже­ния в виде суммы двух составляющих: активной составляющей U _а, совпадающей с векто­ром тока I, и реактивной составляющей U _р, перпенди­ку­лярной к вектору тока (рис. 54а):

		б) треугольник сопротивлений
		Рис. 54

Из геометрии рис. 54а следуют соотношения:

, , .

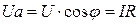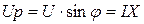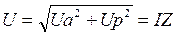Треугольник, составленный из векто­ров 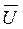, , 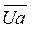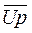получил назва­ние треугольника напряжений (рис. 54а).

Если стороны треугольника напряжений разделить на ток I, то полу­чится новый треугольник, подобный исходному, но сторонами которого явля­ются полное сопротивление Z, активное сопротивление R и реактивное сопро­тивле­ние X. Треугольник со сторонами Z, R, X называется треугольником со­против­лений (рис. 54б). Из треугольника сопротивлений следуют соотношения: R = Z ×cos φ, X = Z ×sin φ, , .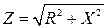

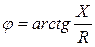Параллельной схеме замещения соответствует представление вектора тока в виде суммы двух составляющих: активной составляющей I_а, совпадаю­щей с вектором напряже­ния U, и реактивной составляющей I_р, перпендикуляр­ной к вектору U (рис. 55а).

Из геометрии рисунка следуют соотношения:

, , .

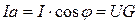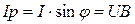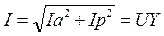Треугольник, составленный из векторов 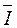, , 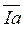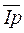получил название тре­угольника токов (рис. 55а).

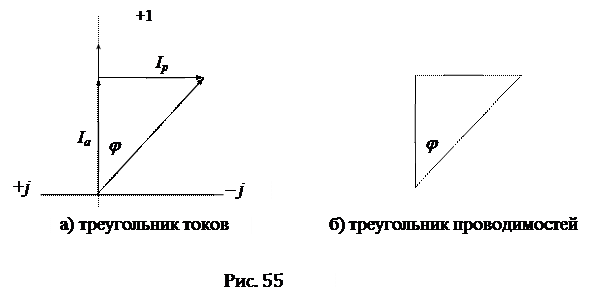Если стороны треугольника токов разделить на напряжение U, то полу­чится новый треугольник, подобный исходному, но сторонами которого явля­ются проводимости: пол­ная – Y, активная - G, реактивная – B (рис. 55б). Тре­угольник со сторонами Y, G, B называется треугольником проводимостей. Из треугольника проводимостей следуют соотношения:

, , , .

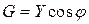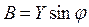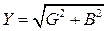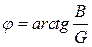Разложение напряжений и токов на активные и реактивные составляющие является математическим приемом и применяется на практике для расчета сравнительно не­сложных цепей пере­менного тока.