2015-07-14
1577
Разберём алгоритм проверки надёжности теста на примере расчёта коэффициента надёжности теста, используя приём расщепления теста на две части по принципу "чётные и нечётные".
Для измерения коэффициента надёжности наиболее часто в психометрических исследованиях используют коэффициент ранговой корреляции Спирмена (rs), применяемый для анализа связи между признаками, измеряемых в порядковых шкалах.
Коэффициент ранговой корреляции Спирмена определяется из уравнения:
где rs – коэффициент ранговой корреляции Спирмена;
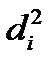– квадрат разности рангов сравниваемых пар переменных (X и Y);
n – Число сопоставляемых пар.
Двигаясь пошагово, по алгоритму проверки надёжности теста, заполним таблицу 1, позволяющую рассчитать коэффициент надёжности теста по формуле 3.1.1..
Таблица 1
Ранжирование и распределение первичных результатов исследования тестом личностной тревожности Спилбергера (n = 20).
| Номер испытуемого | Сумма баллов по чётным заданиям (X) | Сумма баллов по не чётным заданиям (Y) | РАНГ по X | РАНГ по Y | di | d2 i |
| 3,5 | -1,5 | 2,25 | ||||
| 1,5 | 16,5 | 272,25 | ||||
| 5,5 | 3,5 | |||||
| 9,5 | 15,5 | -6 | ||||
| 14,5 | -4,5 | 20,25 | ||||
| 14,5 | 6,5 | 42,25 | ||||
| 14,5 | 2,5 | 6,25 | ||||
| 15,5 | -8,5 | 72,25 | ||||
| 5,5 | 1,5 | |||||
| -10 | ||||||
| 14,5 | 5,5 | |||||
| 9,5 | -9,5 | 90,25 | ||||
| -1 | ||||||
| 5,5 | 2,5 | 6,25 | ||||
| -15 | ||||||
| -8 | ||||||
| -1 | ||||||
| Сумма d2 i = |
Расчёт коэффициента ранговой корреляции Спирмена состоит из ряда этапов:
1) После получения результатов исследования на репрезентативной (однородной) выборке по проверяемой методике (в нашем случае – опросника личностной тревожности Спилбергера – 20 заданий), для каждого испытуемого просчитываются суммы "сырых баллов" для чётных заданий (сумма баллов, набранная по номерам суждений: 2,4,6……18,20) – в нашем случае для 1 испытуемого (таблица 1) – 21 балл, а также суммы "сырых баллов" для не чётных заданий (сумма баллов, набранная по номерам суждений: 1,3,5,7……17,19) – в нашем случае для 1 испытуемого (таблица 1) – 23 балла.
2) Ранжирование рядов переменных. Процедура ранжирования (присвоения порядковых мест) начинается с расположения переменных в ряду по возрастанию их значения. Разным значениям присваиваются ранги, обозначаемые натуральными числами. Если встречаются несколько равных по значению переменных, им присваивается усреднённый ранг. Так в нашем примере рассчитывается "РАНГ по X" для "Сумма баллов по чётным заданиям (X)": 21, можно заметить, что 3 испытуемых (1,12,18) имеют одинаковые баллы – 21. Для определения их ранга необходимо было бы присвоить им ранги 1,2,3. Но одинаковым величинам должны присваиваться одинаковые ранги. Поэтому ранг для значений 21 рассчитывается как среднее арифметическое:
где n – количество слагаемых
Sr – Сумма рангов
И для нашего случая: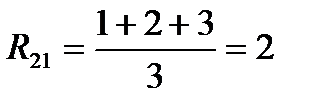 
, т.е. всем величинам 21 присваивается 2 ранг. Присваиваемые ранги для чётной части текста проставляются в столбец РАНГ по X. Аналогичная процедура ранжирования проводится и для Сумма баллов по нечётным заданиям (Y).
3) Заполнение столбца di производится для каждого испытуемого по формуле:
;
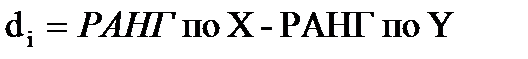4) Складываем результаты последнего столбца, получая величину, соответствующую:
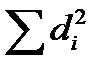
И в нашем случае равную 1284.
5) Подставляем величины в формулу 3.1.1, находим rs – коэффициент ранговой корреляции Спирмена, который является в нашем случае коэффициентом надёжности, и вычисляется:
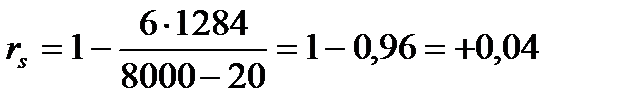
6) Анализируя вычисленный коэффициент надёжности, необходимо ориентироваться в том, что тест считается надёжным, если – коэффициент ранговой корреляции Спирмена находится в пределах от +0,6 до +1,0.
