Теорема Ролля

Теорема (Ролль) (о нуле производной функции, принимающей на концах отрезка равные значения). Если функция f (x) непрерывна на отрезке [ a, b ], дифференцируема на интервале (a, b) и на концах отрезка принимает одинаковые значения f (a) = f (b), то найдется хотя бы одна точка с є (a, b), в которой производная f' (x) обращается в нуль, т.е. f' (с) = 0.

Доказательство. Так как f (x) непрерывна на отрезке [ a, b ], то она, в силу 2-й теоремы Вейерштрасса, достигает на нем своего наибольшего М и наименьшего т значений. Могут представиться два случая.

1. Если М = т, то f (x) постоянна на отрезке [ a, b ] => f '(x) = 0 в любой точке отрезка. Теорема верна.

2. Если М > т, то f (x) достигает хотя бы одно из значений М или т во внутренней точке с интервала (a, b), так как f (a) = f (b) (рис. 2).

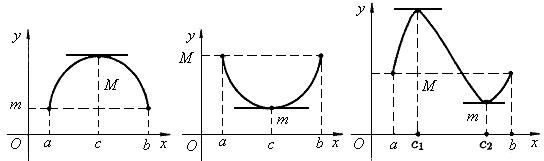
Рис. 2

Даже в том крайнем случае, когда, например, функция f (x) принимает свое наибольшее значение на конце отрезка f (a) = f (b) = M, то наименьшее значение m функция будет принимать внутри отрезка. Следовательно, найдется такая точка с є (a, b), в которой f (с) = m. Тогда по теореме Ферма f' (с) = 0. Теорема доказана.

Геометрический смысл теоремы Ролля: на графике f (x) найдется точка, в которой касательная к графику параллельна оси Ох. На третьем рисунке (рис.2) таких точек две.