Непосредственно из определения дифференциала и правил нахождения производных имеем 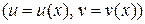 :
:
1. 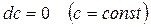 .
.
2. 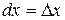 , если x – независимая переменная.
, если x – независимая переменная.
3. 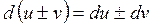 .
.
4. 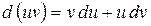 .
.
5. 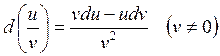 .
.
6. 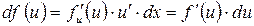 .
.
Найти дифференциалы функций:
Пример 1. 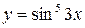 .
.
Находим производную данной функции: 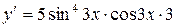 , тогда
, тогда 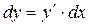 , следовательно,
, следовательно, 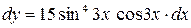 .
.
Пример 2. 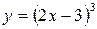 .
.
Находим производную данной функции: 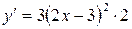 , тогда
, тогда 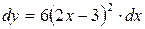
Пример 3. 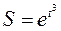 . Дифференциал функции
. Дифференциал функции 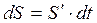 , тогда
, тогда 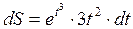
Пример 4. 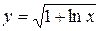 . Дифференциал функции
. Дифференциал функции 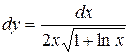 .
.
13. Дифференциал п -го порядка
Дифференциал 2-го порядка от функции 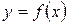 (его обозначают символом
(его обозначают символом 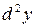 ) – это дифференциал от её дифференциала, рассматриваемого как функция только основного аргумента
) – это дифференциал от её дифференциала, рассматриваемого как функция только основного аргумента 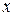 (т.е. при постоянном
(т.е. при постоянном 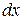 ):
):
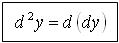
Найдем выражение
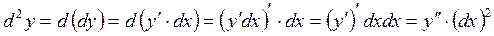 .
.
Таким образом, дифференциал функции 2-го порядка равен произведению её второй производной на квадрат дифференциала независимого переменного.
Аналогично определяется дифференциал 3-го порядка: 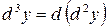 . Если
. Если 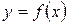 и
и 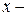 независимая переменная, то
независимая переменная, то 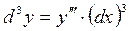 .
.
Определение. Дифференциалом п-го порядка функции 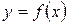 называется дифференциал от дифференциала (п -1) порядка этой функции, т.е.
называется дифференциал от дифференциала (п -1) порядка этой функции, т.е.
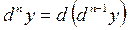 ,
,
Если 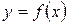 и
и 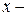 независимая переменная, то
независимая переменная, то 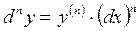
Пример. Найти дифференциал 2-го порядка функции 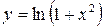 .
.
Решение. Имеем 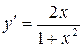 ;
; 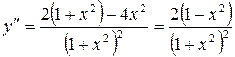 .
.
Тогда 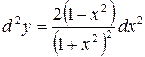 .
.
 2015-07-14
2015-07-14 2999
2999
