Основаны на приближенной замене приращения функции в точке на ее дифференциал ?y ≈ dy.
Как следует из рис.7, погрешность от такой замены при? х →0 является бесконечно малой более высокого порядка по сравнению с? х.
Подставляя в это соотношение формулу для dy и выражение для ?у (?у=f (х+?х) – f (x)), получим
f (х+?х) = f (x) + ?у ≈ f (x) + f' (х)·? х.
Эта формула называется формулой линеаризации и является основной в приближенных вычислениях.
Пример 1. Вычислить приближенное значение корня 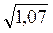 .
.
Решение. Рассмотрим функцию 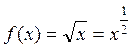 в окрестности точки x =1.
в окрестности точки x =1.
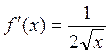 . Принимая ?х = 0,07, получим из формулы линеаризации
. Принимая ?х = 0,07, получим из формулы линеаризации
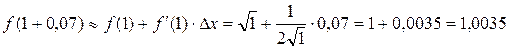
Пример 2. Найти приближенно 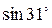 .
.
Решение. Используем формулу линеаризации
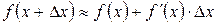 .
.
Пусть 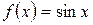 , тогда
, тогда 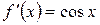 . При малых ?х справедлива формула
. При малых ?х справедлива формула
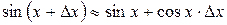
Для (х + Δ х) запишем 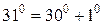 . В радианной мере
. В радианной мере 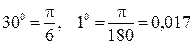 радиан. Тогда
радиан. Тогда 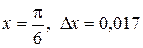 .
.
Используя формулу 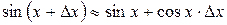 , имеем:
, имеем:
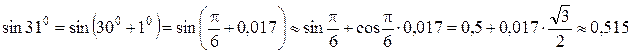 .
.
Пример 3. Вывести приближенную формулу линеаризации (для | ?х |, малых по сравнению с x): 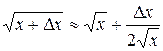 , и с её помощью найти приближенные значения для
, и с её помощью найти приближенные значения для 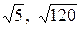 .
.
Решение. Пусть 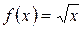 , тогда
, тогда 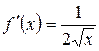 , приращение
, приращение 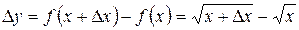 .
.
Следовательно, 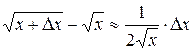 . Отсюда,
. Отсюда, 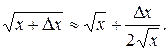
Полагая 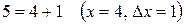 ;
; 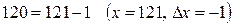 , и применяя формулу линеаризации, имеем:
, и применяя формулу линеаризации, имеем:
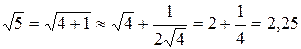 .
.
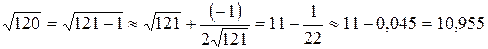 .
.
Пример 4. Вычислить приближенное значение 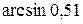 .
.
Решение. Рассмотрим функцию 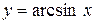 , полагая
, полагая 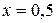 ,
, 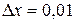 . Применяя формулу
. Применяя формулу 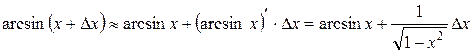 , получаем
, получаем
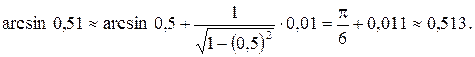
Пример 5. Найти приращение 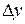 и дифференциал
и дифференциал 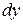 функции
функции 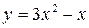 при
при 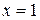 и
и 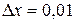 .
.
Решение. Запишем приращение функции 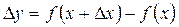 :
:
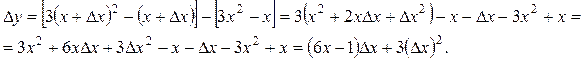
Главная часть приращения, линейная относительно 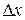 , является дифференциалом
, является дифференциалом 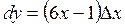 или
или 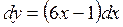 .
.
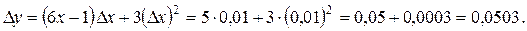
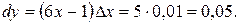
Пример 6. Вычислить приближенное значение площади круга, радиус которого равен 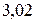 м.
м.
Решение. Воспользуемся формулой 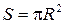 , полагая
, полагая 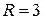 ,
, 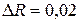 . Имеем
. Имеем 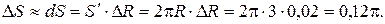
Приближенное значение площади круга составляет
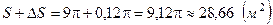 .
.
 2015-07-14
2015-07-14 25004
25004
