Теорема Ферма

Лекция 6. Применение производных к исследованию функций

Если функция f (x) имеет производную в каждой точке отрезка [ а, b ], то ее поведение можно исследовать с помощью производной f' (х).

Рассмотрим основные теоремы дифференциального исчисления, лежащие в основе приложений производной.

Теорема Ферма

Теорема (Ферма) (о равенстве нулю производной). Если функция f (x), дифференцируема на интервале (a, b) и достигает наибольшего или наименьшего значения в точке с є (a, b), тогда производная функции в этой точке равна нулю, т.е. f' (с) = 0.

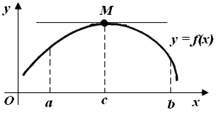
Рис. 1

Доказательство. Пусть функция f (x) дифференцируема на интервале (a, b) и в точке х = с принимает наибольшее значение M при с є (a, b) (рис. 1), т.е.

f (с) ≥ f (x) или f (x) – f (c) ≤ 0 или f (с + Δ х) – f (с) ≤ 0.

Производная f' (x) в точке х = с: .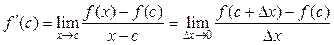

Если x > c, Δ х > 0 (т.е. Δ х → 0 справа от точки с), то 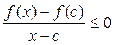и поэтому f' (с) ≤ 0.

Если x < с, Δ х < 0 (т.е. Δ х → 0 слева от точки с), то 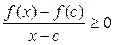, откуда следует, что f' (с) ≥ 0.

По условию f (x) дифференцируема в точке с, следовательно, ее предел при x → с не зависит от выбора направления приближения аргумента x к точке с, т.е. .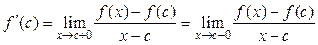

Получаем систему 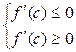, из которой следует f' (с) = 0.

В случае, когда f (с) = т (т.е. f (x) принимает в точке с наименьшее значение), доказательство аналогичное. Теорема доказана.

Геометрический смысл теоремы Ферма: в точке наибольшего или наименьшего значения, достигаемого внутри промежутка, касательная к графику функции параллельна оси абсцисс.