(англ. матем., 1685-1731; шотл. матем. 1698-1746).
Теорема (формула Тейлора). Пусть функция 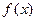
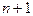 раз дифференцируема на отрезке
раз дифференцируема на отрезке 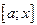 . Тогда
. Тогда 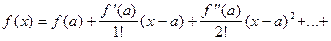
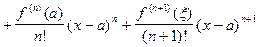 , где
, где 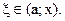
Замечание. Если 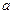 =0, то соответствующая формула называется формулой Маклорена.
=0, то соответствующая формула называется формулой Маклорена.
Теорема. Из формулы Маклорена следуют:
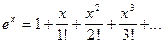 для всех
для всех 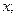
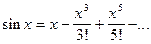 для всех
для всех 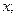
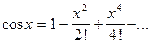 для всех
для всех 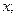
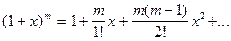 для всех
для всех 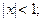
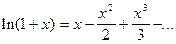
 для всех
для всех 
Пример 39.1. Функцию 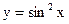 разложим в ряд по степеням
разложим в ряд по степеням 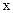 . Имеем:
. Имеем: 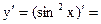 8,14,Ш=
8,14,Ш= 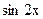 .
. 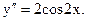
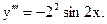
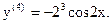
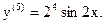
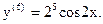 Подставив в формулу Тейлора (при а=0), получим (нули можно не писать):
Подставив в формулу Тейлора (при а=0), получим (нули можно не писать): 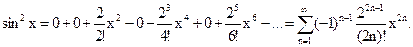
 2015-07-14
2015-07-14 230
230








