Скалярным произведением двух ненулевых векторов 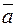 и
и 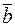 называется число, равное произведению длин этих векторов на косинус угла между ними. Если хотя бы один из векторов нулевой, то скалярное произведение, по определению, полагается равным нулю. Обозначается
называется число, равное произведению длин этих векторов на косинус угла между ними. Если хотя бы один из векторов нулевой, то скалярное произведение, по определению, полагается равным нулю. Обозначается 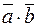 или
или 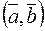 .
.
Из определения
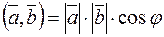 .
.
Так как 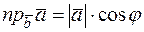 ,
, 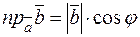 , то
, то
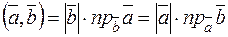 .
.
 Свойства скалярного произведения
Свойства скалярного произведения
1. 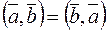 .
.
2. 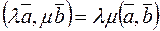 .
.
3. 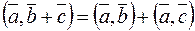 .
.
4. 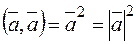 .
.
5. Скалярное произведение двух ненулевых векторов равно нулю, тогда и только тогда, когда векторы перпендикулярны (ортогональны).
 Скалярное произведение в ПДСК
Скалярное произведение в ПДСК
Если известны координаты двух векторов в ПДСК 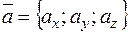 и
и 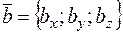 , то
, то
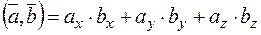 . (7)
. (7)
Отсюда следует необходимое и достаточное условие ортогональности векторов:
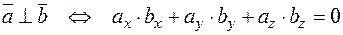 .
.
Угол между векторами 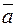 и
и 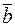 вычисляется по формуле
вычисляется по формуле
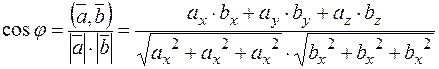 . (8)
. (8)
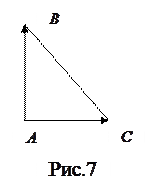
Задача 37. Определить углы треугольника 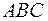 с вершинами
с вершинами 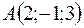 ,
, 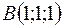 ,
, 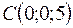 .
.
Решение. Определим угол при вершине  . Он образован векторами
. Он образован векторами  и
и  (Рис.7).
(Рис.7).
 По формуле (8)
По формуле (8)
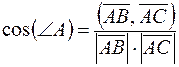 .
.
Найдём координаты указанных векторов по формуле (5). Получим
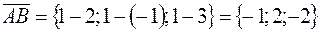 ,
,
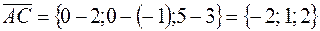 .
.
Вычислим длины векторов 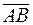 и
и 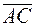 , используя формулу (6):
, используя формулу (6):
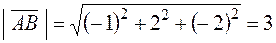 ,
, 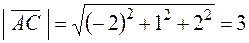 .
.
Вычислим скалярное произведение векторов 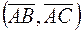 , используя формулу (7)
, используя формулу (7)
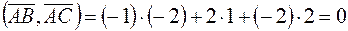 .
.
Так как скалярное произведение равно нулю, то векторы 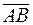 и
и 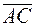 ортогональны и треугольник прямоугольный. Следовательно,
ортогональны и треугольник прямоугольный. Следовательно, 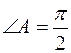 . Так как
. Так как 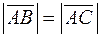 , то треугольник равнобедренный. Значит,
, то треугольник равнобедренный. Значит, 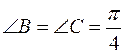 .
.
 2015-07-14
2015-07-14 729
729








