Пусть задана тройка векторов 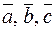 . Будем называть её упорядоченной, если указано, какой из векторов считать первым, какой вторым, какой третьим.
. Будем называть её упорядоченной, если указано, какой из векторов считать первым, какой вторым, какой третьим.
Упорядоченная тройка некомпланарных векторов называется правой, если после приведения их к общему началу, из конца третьего вектора кратчайший поворот от первого ко второму виден совершающимся против часовой стрелки. В противном случае тройка левая.
Векторным произведением вектора 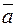 на вектор
на вектор 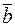 называется вектор
называется вектор 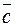 , удовлетворяющий следующими трём условиям:
, удовлетворяющий следующими трём условиям:
1) 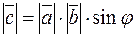 , где
, где 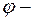 угол между векторами
угол между векторами 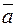 и
и 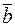 ;
;
2) 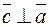 и
и 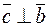 ;
;
3) векторы 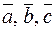 образуют правую тройку.
образуют правую тройку.
Обозначается векторное произведение
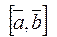
Свойства векторного произведения
1. Векторное произведение двух ненулевых векторов равно нулю, тогда и только тогда, когда векторы коллинеарны.
2. Модуль векторного произведения векторов равен площади параллелограмма, построенного на этих векторах:
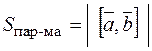 . (9)
. (9)
3. 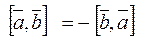 .
.
4. 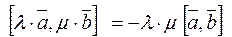 .
.
5. 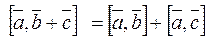
Векторное произведение в ПДСК
Если векторы 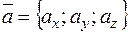 и
и 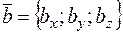 , то векторное произведение вычисляется по формуле:
, то векторное произведение вычисляется по формуле:
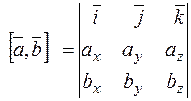 . (10)
. (10)
Задача 43. Вычислить площадь треугольника 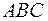 , если
, если 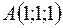 ,
, 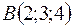 ,
, 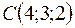 и найти длину высоты треугольника
и найти длину высоты треугольника 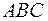 , которая опущена из вершины
, которая опущена из вершины 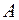 .
.
Решение. Найдём координаты векторов 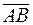 ,
, 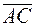 и
и 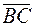 (см. (5)):
(см. (5)):
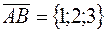 ,
, 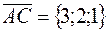 ,
, 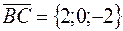
Площадь треугольника 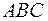 равна половине площади параллелограмма, построенного на векторах
равна половине площади параллелограмма, построенного на векторах 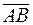 и
и 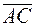 . Найдём площадь параллелограмма по формуле (9). Для этого вычислим векторное произведение этих векторов, используя формулу (10):
. Найдём площадь параллелограмма по формуле (9). Для этого вычислим векторное произведение этих векторов, используя формулу (10):
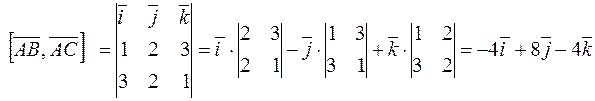 .
.
Следовательно,
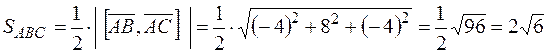 .
.
Из школьного курса геометрии известно, что, 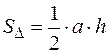 , где
, где 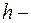 высота треугольника,
высота треугольника, 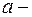 длина стороны, на которую опущена высота. Следовательно,
длина стороны, на которую опущена высота. Следовательно,
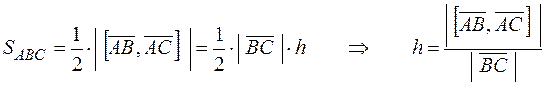 .
.
Тогда
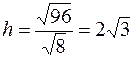 .
.
 2015-07-14
2015-07-14 1062
1062
