Пучком плоскостей называется совокупность плоскостей, проходящих через одну прямую.
Если заданы две различные плоскости из пучка (его образующие)
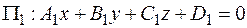 , и
, и 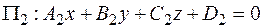 ,
,
то уравнение пучка имеет вид
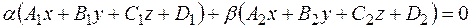 . (8)
. (8)
Задача 59. Написать уравнение плоскости, проходящей через точку 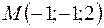 и перпендикулярной к плоскостям
и перпендикулярной к плоскостям 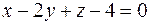 и
и 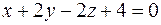 .
.
Решение. Обозначим 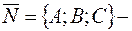 нормальный вектор искомой плоскости
нормальный вектор искомой плоскости 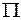 ,
, 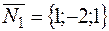 и
и 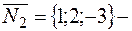 нормальные векторы данных плоскостей. По условию задачи
нормальные векторы данных плоскостей. По условию задачи 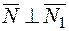 и
и 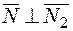 Следовательно,
Следовательно,
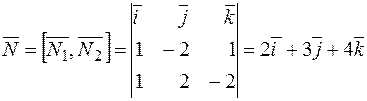 .
.
Подставим координаты точки 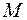 m и вектора нормали
m и вектора нормали 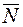 в уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору (7). Получим
в уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору (7). Получим
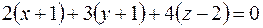 .
.
Отсюда, уравнение искомой плоскости
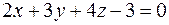 .
.
 2015-07-14
2015-07-14 2114
2114








