Рассмотрим нелинейную систему уравнений
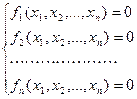 (1.1)
(1.1)
с действительными левыми частями.
Запишем короче систему (1.1). Совокупность аргументов 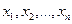 можно рассматривать как
можно рассматривать как 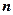 - мерный вектор
- мерный вектор
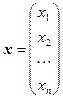 .
.
Аналогично совокупность функций 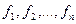 представляет собой также
представляет собой также 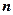 - мерный вектор (вектор-функцию)
- мерный вектор (вектор-функцию)
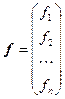 .
.
Поэтому система (1.1) кратко записывается так:
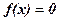 . (1.1/ )
. (1.1/ )
Для решения системы (1.1/ ) будем пользоваться методом последовательных приближений.
Предположим, что найдено 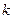 -е приближение
-е приближение
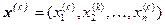
одного из изолированных корней 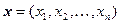 векторного уравнения (1.1/ ).
векторного уравнения (1.1/ ).
Тогда точный корень уравнения (1.1/ ) можно представить в виде
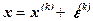 , (1.2)
, (1.2)
где 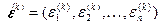 - поправка (погрешность корня).
- поправка (погрешность корня).
Подставляя выражение (1.2) в уравнение (1.1/ ), будем иметь:
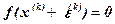 . (1.3)
. (1.3)
Предполагая, что функция 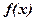 непрерывно дифференцируема в некоторой области, содержащей
непрерывно дифференцируема в некоторой области, содержащей 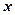 и
и 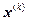 , разложим левую часть уравнения (1.3) по степеням малого вектора
, разложим левую часть уравнения (1.3) по степеням малого вектора 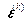 , ограничиваясь линейными членами,
, ограничиваясь линейными членами,
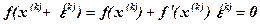 . (1.4)
. (1.4)
или, в развернутом виде,
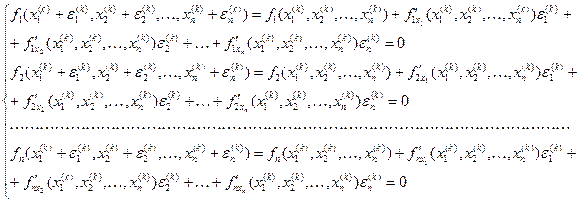 (1.4/ )
(1.4/ )
Из формул (1.4) и (1.4/ ) вытекает, что под производной 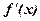 следует понимать матрицу Якоби системы функций
следует понимать матрицу Якоби системы функций 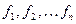 относительно переменных
относительно переменных 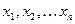 , т.е.
, т.е.
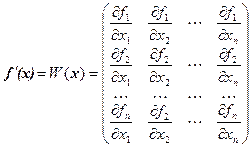 ,
,
или в краткой записи
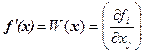
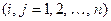 .
.
Система (1.4/) представляет собой линейную систему относительно поправок 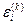
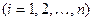 с матрицей
с матрицей 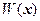 , поэтому формула (1.4) может быть записана в следующем виде:
, поэтому формула (1.4) может быть записана в следующем виде:
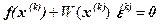 .
.
Отсюда, предполагая, что матрица 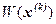 - неособенная, получим:
- неособенная, получим:
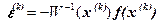 .
.
Следовательно,
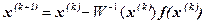
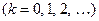 , (1.5)
, (1.5)
где за 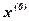 можно взять грубое значение искомого корня.
можно взять грубое значение искомого корня.
При практическом применении метода Ньютона для решения нелинейных систем вычисления по формуле (1.5) прекращают, когда
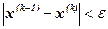 . (1.6)
. (1.6)
Итак, исходя из вышеизложенного, запишем алгоритм метода Ньютона:
1. Определяем начальное приближение 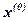 .
.
2. Уточняем значение корня по формуле (1.5).
3. Если условие (1.6) выполняется, то задача решена и 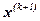 - корни системы нелинейных уравнений, иначе переходим к п. 2.
- корни системы нелинейных уравнений, иначе переходим к п. 2.
Будем считать, что функции 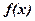 нелинейной системы (1.1/ ) и матрица их производных
нелинейной системы (1.1/ ) и матрица их производных 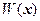 уже определены, тогда блок-схема алгоритма решения этой системы имеет вид:
уже определены, тогда блок-схема алгоритма решения этой системы имеет вид:
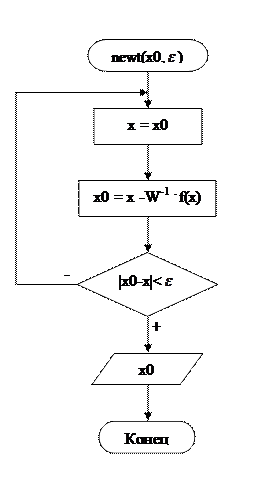

1.2. Реализация метода Ньютона в|посредством| MathCad
Пример. Решить нелинейную систему уравнений методом Ньютона
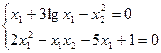
с точностью 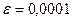 .
.
Приведем решение нелинейной системы уравнений с помощью|посредством| программного комплекса MathCad:
Номер первой строки (столбца) матрицы или первой компоненты вектора хранится в MathCad в переменной ORIGIN. По умолчанию в MathCad координаты векторов, столбцы и строки матрицы нумеруются начиная с 0 (ORIGIN:=0). Поскольку в математической записи чаще используется нумерация с 1, здесь и в дальнейшем перед началом работы с матрицами будем определять значение переменной ORIGIN равным 1, т.е. будем выполнять команду ORIGIN:=1. Далее определяем функции F1 и F2 нелинейной системы и находим графическое решение системы.

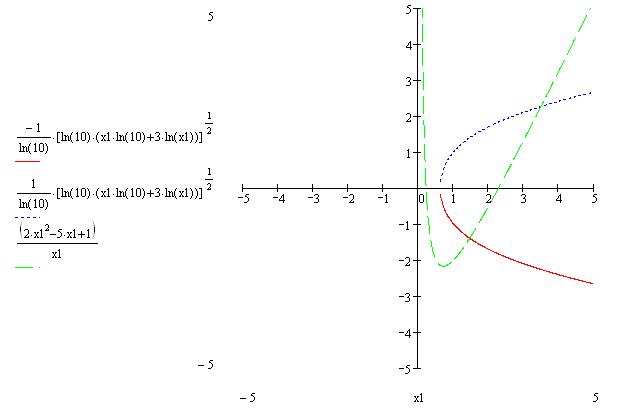
Процесс отыскания корней системы при помощи метода Ньютона организован в виде функции, входные параметры которой – вектор начальных приближений x0 и точность вычислений (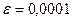 ), где за x0 можно взять грубое значение искомого корня – приблизительные координаты точки пересечения графиков функций:
), где за x0 можно взять грубое значение искомого корня – приблизительные координаты точки пересечения графиков функций: 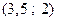 – грубое значение первого корня, затем
– грубое значение первого корня, затем 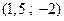 – грубое значение второго корня.
– грубое значение второго корня.

 2015-07-14
2015-07-14 519
519








