Простейшие приемы построения разностных схем

Дифференциальные уравнения в частных производных имеют широкое приложение в математической физике, гидродинамике, акустике и т. д. Многие задачи механики сплошной среды сводятся к решению дифференциальных уравнений в частных производных. В большинстве случаев получить решение таких уравнений в явном виде не представляется возможным, поэтому широко применяются приближенные методы. Построение различных схем методом конечных разностей в случае уравнений в частных производных зависит от типа уравнений и вида граничных условий.

Пусть G – некоторая область изменения независимых переменных x, y, ограниченная контуром Г. Говорят, что в области G задано линейное дифференциальное уравнение второго порядка для функции U(x,y), если для любой точки из области G имеет место соотношение:

AU_xx+2BU_xy+CU_yy+DU_x+EU_y+F=0. (9.1)

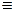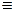Коэффициенты уравнения, вообще говоря, зависят от x, y. Если A B C 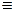0, а D 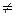0 и E 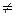0, то уравнение (9.1) имеет первый порядок и называется уравнением переноса. Обозначим Q= B²+ AC, Q= Q(x, y). Уравнение называется эллиптическим, если Q<0; параболическим, если Q>0, и гиперболическим - если Q=0 для всех (x,y) из области G.

Например, уравнение Пуассона 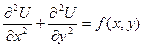является уравнением эллиптического типа (Q<0), действительно, так как A =1, B =0, C =1, то Q = -1.

Уравнение теплопроводности 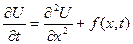является уравнением параболического типа (Q=0), действительно, так как A =1, B =0, C =0, то Q =0.

Волновое уравнение 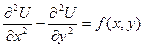является уравнением гиперболического типа (Q >0), действительно, так как A =1, B =0, C =-1, то Q =1.