Рассмотрим дифференциальное уравнение, заданное в некоторой области D, ограниченной контуром Г:
LU = f, (9.2)
где U - решение (9.2). Множество Dh ={ Mh } состоящее из изолированных точек Mh, принадлежащих замкнутой области D, называется сеткой, а точки Mh - узлами сетки. Функция, определенная в узлах сетки, называется сеточной функцией Uh . На практике, как правило, можно вычислить только приближенное сеточное значение функции U(h).
Для нахождения U(h) строим систему численных уравнений:
Lh(U(h)) = f(h) , (9.3)
где Lh – разностный оператор, соответствующий оператору L, f(h) – разностный аналог правой части.Уравнение (9.3) является разностной схемой.
Таким образом, в методе сеток происходит замена пространства V (пространства непрерывных в D функций U) на пространство Vh (пространство, образованное совокупностью сеточных функций Uh, определенных на Dh.). В линейных пространствах Vh и Fh введем нормы 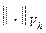 и
и 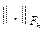 , которые являются сеточными аналогами норм в пространстве V и F.
, которые являются сеточными аналогами норм в пространстве V и F.
Определение. Говорят, что разностная схема (9.3) является сходящейся, если при h ® 0 выполняется условие
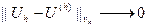 . (9.4)
. (9.4)
Если выполнено условие 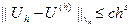 (с=const, s>0), то говорят, что имеет место сходимость со скоростью порядка s.
(с=const, s>0), то говорят, что имеет место сходимость со скоростью порядка s.
Определение. Говорят, что разностная схема (9.3) аппроксимирует задачу (9.2) на решение U, если
Lh(Uh) = f(h)+d f(h) (9.5)
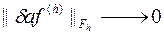 при h ® 0,
при h ® 0,
величина d f(h) называется погрешностью аппроксимации.
Если 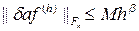 (M=const, β >0), то говорят, что разностная схема (9.3) аппроксимирует задачу (9.2) с погрешностью порядка β относительно h.
(M=const, β >0), то говорят, что разностная схема (9.3) аппроксимирует задачу (9.2) с погрешностью порядка β относительно h.
Определение. Разностная схема (9.3) называется устойчивой, если существует такое h0 >0, что для всех h<h0 и любых f(h)ÎFh выполняются условия:
1) разностная схема (9.3) имеет единственное решение;
2) 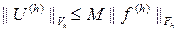 , где M – постоянная, не зависящая от h и f(h).
, где M – постоянная, не зависящая от h и f(h).
Теорема. Пусть разностная схема Lh(U(h)) = f(h) аппроксимирует задачу LU = f на решение U с порядком s> 0 относительно h и устойчива. Тогда эта схема будет сходящейся и порядок ее сходимости будет совпадать с порядком аппроксимации, т. е. будет справедлива оценка:
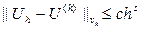 , (9.6)
, (9.6)
где с – постоянная, не зависящая от h.
 2015-07-14
2015-07-14 1111
1111
