1. Аналитически показать, что при k (x) =const, q (x) =const, u (x) - многочлен второй степени, разностная схема (8.11) дает точное решение.
2. Показать, что приведенные формулы численного интегрирования для коэффициентов дают 2 -й порядок точности:
di=q (xi) +o (h2), ji=f (xi) +o (h2), ai=k (xi) +o (h2).
3. Выполнить программную реализацию интегро-интерполяционного метода и на ее основе проверить п.1.
4. Построить собственный пример (8.11) на классе функций: k (x), q (x) - линейные. Сравнить численное решение с аналитическим.
5. В схеме (8.11) использовать следующие коэффициенты:
k (x) =ax+b, q (x) =cx+e, u (x) =rx2+px+g;
k (x) =ax+b, q (x) =const, u (x) =e-lx (рассмотреть два случая: 0<l<1 и l>1).
6. Составить разностную схему для следующей краевой задачи:
p (x) u² (x) +q (x) u¢ (x) +r (x) u (x) = f (x),
a1 u¢ (a) +b1 u (a) =g1,
a2 u¢ (b) +b2 u (b) =g2,
a<x<b.
7. Для данной краевой задачи найти аналитическое решение методом Галеркина или методом наименьших квадратов и сравнить полученное решение с найденным приближенным решением.
8. Записать разностную схему для одного из вариантов краевой задачи для обыкновенного дифференциального уравнения и решить методом прогонки.
Варианты заданий
1. 
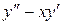 + 2xy=0,8 2.
+ 2xy=0,8 2. 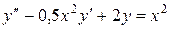
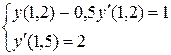
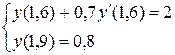
3. 
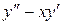 + 2y=x+1 4.
+ 2y=x+1 4. 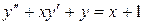
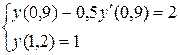
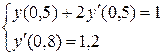
5. 
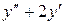 - xy=x2 6.
- xy=x2 6. 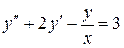
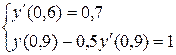
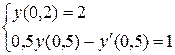
7. 
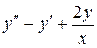 = x+0,4 8.
= x+0,4 8. 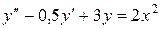
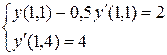
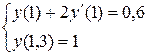
9. 
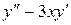 + 2y=1,5 10.
+ 2y=1,5 10. 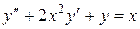
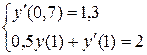
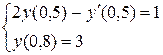
11. 
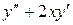 - 2y=0.6 12.
- 2y=0.6 12. 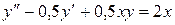
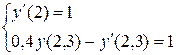
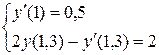
13. 
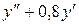 - xy=1,4 14.
- xy=1,4 14. 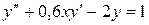
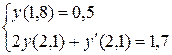
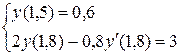
 2015-07-14
2015-07-14 443
443








