Метод Гюна. Проінтегруємо ліву і праву частини рівняння (1.1) в межах від t0 до t1:
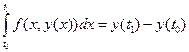 . (1.4)
. (1.4)
Із рівняння (1.4) знайдемо:
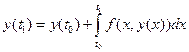 . (1.5)
. (1.5)
Інтеграл, який знаходиться у правій частині рівняння (1.5), можна наближено обчислити за формулою трапецій:
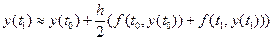 . (1.6)
. (1.6)
Права частина рівняння (1.6) вимагає знання 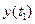 , яке знайдемо, скориставшись методом Ейлера. Із формули (1.3) для k=0 отримаємо:
, яке знайдемо, скориставшись методом Ейлера. Із формули (1.3) для k=0 отримаємо:
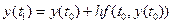 .
.
З врахуванням значення 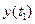 формула (1.6) набуде такого вигляду:
формула (1.6) набуде такого вигляду:
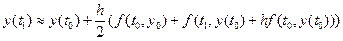 .
.
Тепер, зробивши заміну 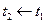 ,
, 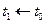 , генеруємо процес, який наближує праву відповідному розв’язку Задачі Коші
, генеруємо процес, який наближує праву відповідному розв’язку Задачі Коші 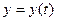 .
.
Для k -го кроку обчислень будемо мати:
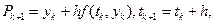 (1.7)
(1.7)
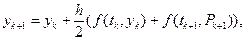 (1.8)
(1.8)
де k=0,1,2…
Залишковий член у формулі трапецій, який використовують для наближення інтервалу в (7.6), дорівнює:
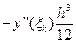 . (1.9)
. (1.9)
Метод Рунге-Кутта. Ідея побудови методів Рунге-Кутта p - го порядку полягає в отриманні наближеного числового розв’язку задачі Коші за формулою:
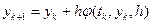 , (1.10)
, (1.10)
де 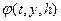 - деяка функція, яка наближує відрізок ряду Тейлора до p -го порядку і не вміщує часткових похідних функції
- деяка функція, яка наближує відрізок ряду Тейлора до p -го порядку і не вміщує часткових похідних функції 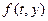 .
.
Якщо в (1.10) замінити 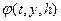 на
на 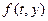 , то отримаємо метод Ейлера, тобто метод Ейлера можна вважати частковим випадком методів Рунге-Кутта, коли p=1.
, то отримаємо метод Ейлера, тобто метод Ейлера можна вважати частковим випадком методів Рунге-Кутта, коли p=1.
Для побудови методів Рунне-Кутта вище першого порядку функцію 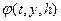 вибирають як таку, що залежить від певних параметрів, які вибирають шляхом порівняння виразу (1.10) з многочленом Тейлора для
вибирають як таку, що залежить від певних параметрів, які вибирають шляхом порівняння виразу (1.10) з многочленом Тейлора для 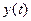 з бажаним порядком степеня.
з бажаним порядком степеня.
Розглянемо випадок p=2 і візьмемо функцію 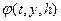 з наступною структурою:
з наступною структурою:
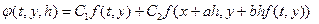 . (1.11)
. (1.11)
Розкладемо функцію двох змінних 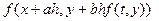 в ряд Тейлора, обмежившись лінійними членами:
в ряд Тейлора, обмежившись лінійними членами:
 .
.
Її підстановка в (1.11) дає:
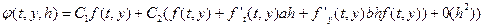
де 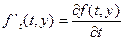 ,
, 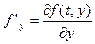 .
.
Підставивши останній вираз в (1.10), отримаємо:
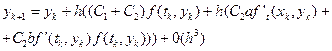 . (1.12)
. (1.12)
Розкладемо тепер функцію 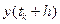 в ряд Тейлора, враховуючи члени першого і другого порядків:
в ряд Тейлора, враховуючи члени першого і другого порядків:
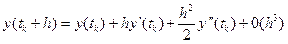 . (1.13)
. (1.13)
Оскільки 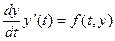 , то
, то 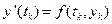 .
.
Знайдемо другу похідну 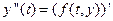 . За формулою повної похідної будемо мати:
. За формулою повної похідної будемо мати:
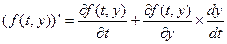 .
.
Враховуючи значення 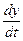 , отримаємо:
, отримаємо:
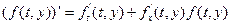 .
.
Отже:
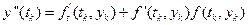 .
.
Тепер значення 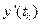 і
і 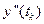 можемо підставити у вираз (1.13). У результаті отримаємо:
можемо підставити у вираз (1.13). У результаті отримаємо:
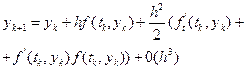 . (1.14)
. (1.14)
Порівнюючи між собою вирази (1.12) і (1.14) приходимо до висновку, що:
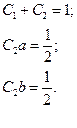
Отримана система із трьох рівнянь, яка вміщує чотири невідомих. Це означає, що один із параметрів вільний і його можна вибрати довільним. Візьмемо 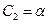 , де
, де 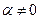 . Тоді:
. Тоді:
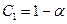 ,
, 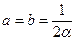 .
.
У результаті підстановки значень C1, C2 , a і b у формулу (1.11) маємо:
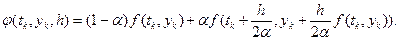
Отриманий результат дає підставу ітераційну процедуру (1.10) записати у такому вигляді:
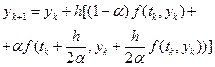 . (1.15)
. (1.15)
Якщо в (1.15) 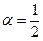 , то:
, то:
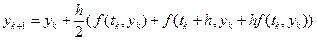 , (1.16)
, (1.16)
а при 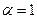 маємо:
маємо:
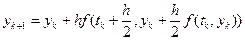 . (1.17)
. (1.17)
Ітераційна процедура (1.16) носить назву метода Хойна, а (1.17) – породжує метод середньої точки.
Аналіз методів Рунге-Кутта другого порядку дає уявлення в якій формі слід шукати метод Рунге-Кутта довільного порядку.
За аналогією (1.11) можемо записати:
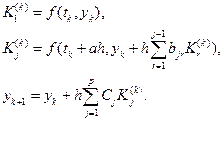 (1.18)
(1.18)
Найпоширенішим із сімейства методів (1.18) є метод четвертого порядку (p=4) або просто метод Рунге-Кутта, який породжує таку ітераційну процедуру:
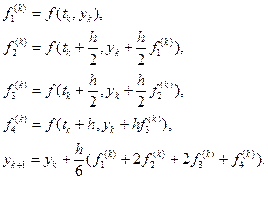 (1.19)
(1.19)
Метод Рунге-Кутта дає похибку накопичення четвертого порядку – 0(h4).
Бажання підвищити точність методу Рунге-Кутта привело до появи різних його версій. Одна із них метод Кутта-Мерсона з вибором кроку на кожній із ітерацій.
На k - ому кроці розв’язку задачі Коші послідовно обчислюють:
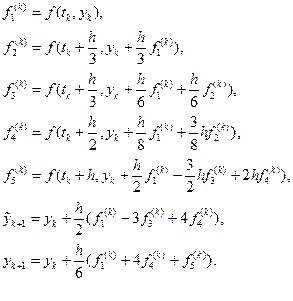 (1.20)
(1.20)
Після цього підраховують величину
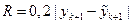 , (1.21)
, (1.21)
і, якщо 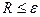 , то вважають, що в точці
, то вважають, що в точці 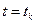 отриманий розв’язок задачі Коші з точністю
отриманий розв’язок задачі Коші з точністю 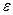 . У тому випадку, коли
. У тому випадку, коли 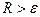 крок h зменшують вдвічі
крок h зменшують вдвічі 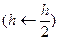 і знову обчислюють значення
і знову обчислюють значення 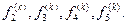 При переході до наступного кроку k+1 здійснюється перевірка на можливість збільшення кроку. Якщо
При переході до наступного кроку k+1 здійснюється перевірка на можливість збільшення кроку. Якщо 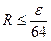 , то
, то 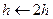
3 ЗАВДАННЯ
1 Чисельно розв’язати дифрівняння з таблиці.
2 Записати всі співвідношення, що необхідні для розробки алгоритму програми.
3 Написати програму і розрахувати на ЕОМ значення кореня зазначеного рівняння.
4 Розробити програму для розв’язку даного рівняння. Розрахувати на ЕОМ значення кореня. Порівняти результати двох методів.
4 КОНТРОЛЬНІ ПИТАННЯ
1 Що називається коренем рівняння?
2 Визначення простого і кратного кореня.
3 Основні етапи пошуку кореня.
4 Визначення швидкості і порядку збіжності чисельного методу пошуку кореня.
5 Визначення інтервалу невизначеності кореня.
6 Метод Ейлера.
7 Метод Гюна.
8 Метод Рунге-Кутта.
5 ТАБЛИЦЯ ІНДИВІДУАЛЬНИХ ЗАВДАНЬ
| № | f(x,y) | y0 |
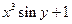
| 0.0 | |
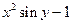
| 0.1 | |
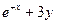
| 2.0 | |
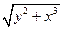
| 0.3 | |
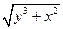
| 0.4 | |
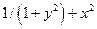
| 0.0 | |
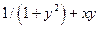
| 0.1 | |
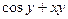
| 0.2 | |
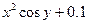
| 0.3 | |
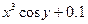
| 0.4 | |
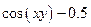
| 0.5 | |
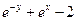
| 0.0 | |
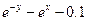
| 0.5 | |
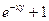
| 0.4 | |
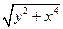
| 0.3 |
 2015-07-14
2015-07-14 287
287








