ЗМІСТ
Загальні методичні вказівки ………………………………….4
| Лабораторна робота №1 Чисельний розв'язок диференціальних рівнянь методами Ейлера, Гюна і Рунге-Кутта………………………………………………. | |
| Лабораторна робота №2 Чисельний розв'язок систем диференціальних рівнянь……………………….. | |
| Лабораторна робота №3 Чисельний розв'язок гіперболічних рівнянь…………………………………… | |
| Лабораторна робота №4 Чисельний розв'язок параболічних та еліптичних рівнянь…………………… | |
| Лабораторна робота № 5. Знаходження екстремальних значень функції однієї змінної методом пошуку і золотого перерізу……………………………... | |
| Лабораторна робота № 6. Знаходження екстремальних значень функції симплексним методом Нелдера-Міда…………………………………………….. | |
| Лабораторна робота №7. Знаходження екстремальних значень функції градієнтними методоми…………………………………………………… | |
| Лабораторна робота №8. Моделювання лінійних систем у середовищі MatLab……………………………. | |
| Лабораторна робота №9. Моделювання стохастичних систем з «кольоровим» вхідним сигналом у середовищі MatLab………………………... | |
| Лабораторна робота №10 Складання та моделювання гідравлічних і теплових об’єктів……… | |
| Перелік рекомендованих джерел…………………… |
ЗАГАЛЬНІ МЕТОДИЧНІ ВКАЗІВКИ
Лабораторні роботи з дисципліни “Числові методи і моделювання на ЕОМ” проводяться у лабораторії, оснащеній персональними комп’ютерами під операційною системою Windows.
До початку лабораторної роботи студент повинний підготувати протокол даної роботи, який має містити назву, мету, завдання, теоретичну частину даної роботи й текст програми. Перед виконанням роботи студент обов’язково має отримати допуск у викладача.
Студенти, які не підготували протокол із текстом програми, до виконання роботи не допускаються.
Захист і оцінювання лабораторної роботи має відбуватися по завершенню виконання роботи в кінці навчальної пари. Оцінювання лабораторної роботи здійснюється за теоретичними знаннями, які набувають студенти під час виконання роботи.
Для зарахування роботи студент має представити звіт, оформлений за наступними вимогами:
1 Назва лабораторної роботи.
2 Індивідуальне завдання.
3 Теоретична частина необхідна для виконання індивідуального завдання.
4 Тексти програм.
5 Таблиця результатів розрахунку на ЕОМ.
Зауваження: Пункти 1-4 звіту, а також таблиця пункту 5 без чисельних результатів повинні бути оформлені до початку виконання лабораторної роботи.
За невчасне виконання роботи або здачу звіту оцінка знижується.
ЛАБОРАТОРНА РОБОТА №1
Чисельний розв'язок диференціальних рівнянь методами Ейлера, Гюна і РунГе-Кутта (4 год.)
1 МЕТА РОБОТИ
1 Вивчення основних визначень і положень теорії чисельного розв'язку диференціальних рівнянь.
2 Вивчення основних методів чисельного розв'язку диференціальних рівнянь.
3 Розробка програм і розв'язок на ЕОМ диференціальних рівнянь.
2 КОРОТКІ ТЕОРЕТИЧНІ ВІДОМОСТІ
1 Основні визначення
Процес проектування автоматичних систем керування передбачає створення математичних моделей технологічних об’єктів. Такі моделі у більшості випадків мають вигляд диференціальних рівнянь. Для отримання відомостей про властивості об’єктів необхідно знати розв’язки їх моделей. Отримати аналітичний розв’язок таких моделей можна тільки в окремих випадках. У переважній більшості для розв’язку диференціальних рівнянь застосовують числові методи.
Методи розв’язку диференціальних рівнянь
Метод Ейлера. Він має обмежене застосування із-за великої похибки, яка накопичується у процесі обчислень.
Отже, будемо розглядати звичайне диференціальне рівняння першого порядку
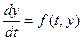 , (1.1)
, (1.1)
з початковою умовою
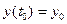 , (1.2)
, (1.2)
де 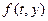 - деяка відома у загальному випадку нелінійна функція двох аргументів.
- деяка відома у загальному випадку нелінійна функція двох аргументів.
Будемо вважати, що для даної задачі (1.1), (1.2), яка носить назву задачі Коші виконуються вимоги, які забезпечують існування і єдність на відрізку 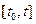 її розв’язку
її розв’язку 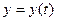 .
.
Допустимо, що 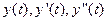 неперервні. Використовуючи теорему Тейлора, розкладемо функцію
неперервні. Використовуючи теорему Тейлора, розкладемо функцію 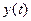 у ряд Тейлора в околі точки
у ряд Тейлора в околі точки 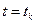 . Для кожного значення
. Для кожного значення 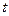 існує таке
існує таке 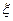 , яке лежить між
, яке лежить між 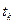 і
і 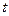 , що
, що
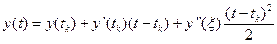 .
.
У відповідності з (6.1) 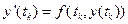 .
.
Тому 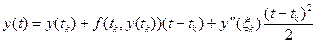 .
.
Нехай 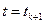 і
і 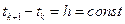 , а
, а 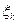 - точка, яка лежить між
- точка, яка лежить між 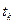 і
і 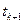 . Тоді
. Тоді
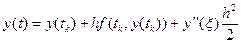 .
.
Якщо довжина кроку h вибрана досить малою, то членом другого порядку можна знехтувати і отримати
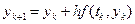 , (1.3)
, (1.3)
де 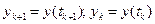 .
.
Ітераційна процедура (1.3) і є наближенням Ейлера для задачі (1.1), (1.2) при цьому 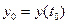 .
.
Як випливає із формули (1.3) кожна наступна ордината, починаючи із 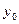 , обчислюється шляхом додавання до неї площі прямокутника
, обчислюється шляхом додавання до неї площі прямокутника 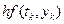 (рис 1.1).
(рис 1.1).
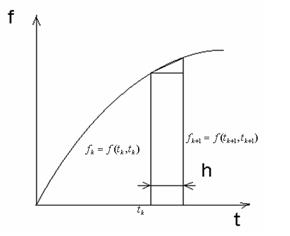
Рисунок 1.1- Ілюстрація процесу утворення
 2015-07-14
2015-07-14 305
305







