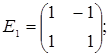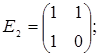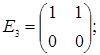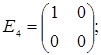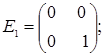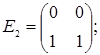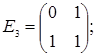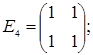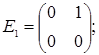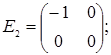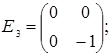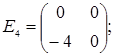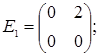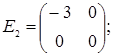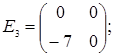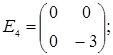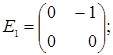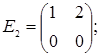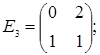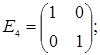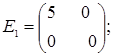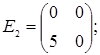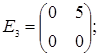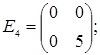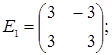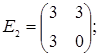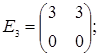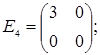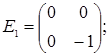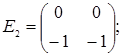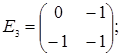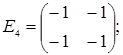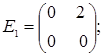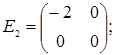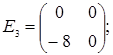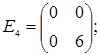Дане рівняння визначає еліпсоїд у просторі. Знаходимо його найпростіше рівняння:
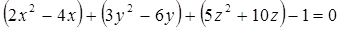
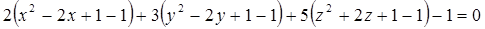
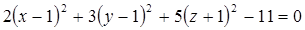
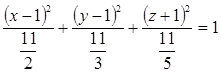
Відповідь: 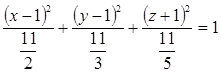 .
.
10.
З’ясувати геометричний зміст рівняння: x2 = 2pz
Розв’язання
Дане рівняння на площині є рівнянням пароболи, симетричної відносно осі. У просторі – це рівняння є рівнянням параболічного циліндру, розташованого вздовж осі.
 | 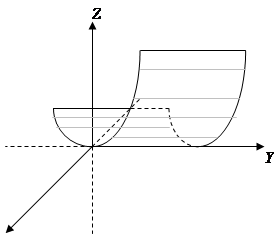 | ||||
| |||||
Контрольна робота № 2
I. Обчислити вирази
1. 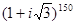 ; 3.
; 3. 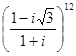 ; 5.
; 5. 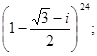
2. 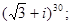 4.
4. 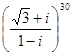 ; 6.
; 6. 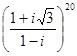 ; 10.
; 10. 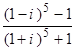
7. 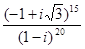 ; 8.
; 8. 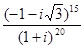 ; 9.
; 9. 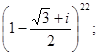
II. Представити у вигляді многочлена першого степеня від тригонометричних функцій кутів, кратних х:
1. sin3x; 2. sin4x; 3. cos5x; 4.cos6x; 5. sin3x·cos5x;
6. 3sin4xcos3x; 7. 5cos3xsin2x; 8. sin7x; 9. cos4xsin3x; 10.sin5x.
III. Обчислити суми:
1. cos x + cos 2x+ …+ cos nx; 5. cos 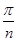 +cos
+cos 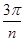 +cos
+cos 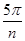 +…+cos
+…+cos 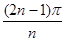
2. sin x + sin 2x + …+ sin nx; 6. sin 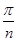 +sin
+sin 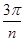 +sin
+sin 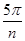 +…+sin
+…+sin 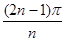
3. sin x + 2sin 2x + …+ nsin nx; 7. cos2 x + cos2 2x+ …+ cos2 nx;
4. cos x +2cos 2x+ …+ ncos nx; 8. sin2 x + sin2 2x + …+ sin2 nx;
9. 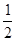 + cos x + cos 2x+ …+ cos nx; 10. 1+acosφ+a2cos2φ+…+akcoskφ.
+ cos x + cos 2x+ …+ cos nx; 10. 1+acosφ+a2cos2φ+…+akcoskφ.
IV. 1. Знайти суму всіх коренів 6-го степеня з одиниці.
2. Довести, що первісний корінь n-го степеня з одиниці має порядок n.
3. Знайти суму всіх коренів 15-го степеня з одиниці.
4. Знайти суму всіх первісних коренів 10 степеня з одиниці.
5. Знайти суму всіх первісних коренів 15-го степеня з одиниці.
6. Знайти необхідну і достатню умови того, щоб кожен первісний корінь nm-го степеня з одиниці можна було зобразити у вигляді добутку первісних коренів n-го і m-го степенів з одиниці.
7. Знаючи, що 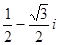 є одним із значень
є одним із значень 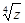 , знайти всі значення
, знайти всі значення 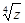 .
.
8. Знаючи, що 2+і є одним із значень 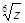 , знайти всі значення
, знайти всі значення 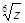 .
.
9. Знайти суму всіх коренів n-го степеня з одиниці.
10. Знайти суму всіх первісних коренів 24-го степеня з одиниці.
V. Дана система лінійних неоднорідних рівнянь:
(*) 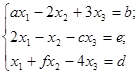
1) Знайти ранг матриці А системи (*) А= 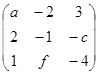 .
.
2) Дослідити систему на сумісність.
3) Обчислити визначник матриці А способом:
а) зведенням до трикутного вигляду;
б) розкладанням за елементами першого рядка.
4) Розв'язати систему рівнянь методом Гауса, методом Крамера;
5) Знайти матрицю, обернену до матриці А системи двома способами:
а) за допомогою матриці А*- приєднаної до матриці А: 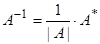
б) за допомогою комбінованої матриці: (А/Е)~(Е/A-1).
6) Записати систему (*) в матричному вигляді та розв’язати її в матричному вигляді.
Таблиця значень параметрів системи (*)
 Варіант параметр Варіант параметр | ||||||||||
| a | ||||||||||
| b | ||||||||||
| c | -4 | -3 | -5 | -2 | ||||||
| e | -2 | -4 | -2 | -2 | -4 | |||||
| f | -5 | |||||||||
| d | -1 | -2 | -2 | -3 | -8 | -1 |
VI. За допомогою теореми про накладання розв’язків знайти загальний розв’язок системи лінійних рівнянь (*).
(*) 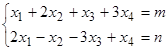
Таблиця значень параметрів системи (*)
 Варіант параметр Варіант параметр | ||||||||||
| m | ||||||||||
| n | -1 | -3 | -2 | -5 | -2 |
Зразки розв’язання задач контрольної роботи №2
1. Обчислити вираз: (1-і 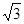 )30.
)30.
Розв’язання: Представимо комплексне число z=1-i 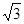 в тригонометричній формі та застосуємо формулу Муавра піднесення комплексного числа до n-го степеня. Тригонометрична форма комплексного числа має вигляд: z=r(cos φ+isin φ), де
в тригонометричній формі та застосуємо формулу Муавра піднесення комплексного числа до n-го степеня. Тригонометрична форма комплексного числа має вигляд: z=r(cos φ+isin φ), де 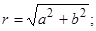
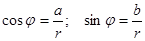 ;
;
в нашому випадку а=1; b=- 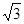 ; i=
; i= 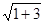 =2;
=2; 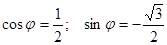 .
.
Звідси 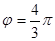 ; Тоді z=2(cos
; Тоді z=2(cos 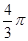 +isin
+isin 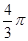 ).
).
z30= 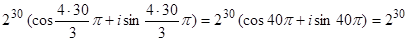 .
.
Відповідь: 230.
2. Представити у вигляді многочлена першого степеня від тригонометричних функцій кутів, кратних х cos3х.
Розв'язання: Розглянемо комплексне число z = cos x + isin x.
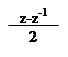 | |||
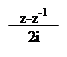 | |||
Тоді cos x =; sin x =;
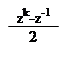 | 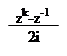 | ||
cos kx =; sin kx =;
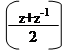 | 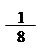 | 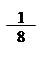 | |||
cos3x = = (z3 + 3z2 * z-1 + 3z-2 * z +z-3) = ((z3 + z-3) + 3(z + z-1)) =
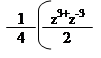 | |||||
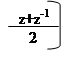 | 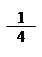 |
= +3 = (cos 3x + 3cos x);
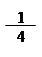 |
Відповідь: (cos 3x + 3cos x).
3. Обчислити суму: cos x + cos 2x + … + cos nx.
Розв'язання: Позначимо через S = cos x + cos 2x + … + cos nx,
T = sin x + sin 2x + … + sin nx.
Тоді S + Ti = (cos x + isin x) + (cos 2x + isin 2x) + … + (cos nx + isin nx);
cos x + isin x = a.
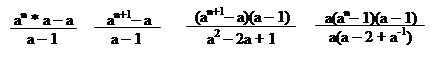 |
S+Ti = a + a2 +…+ an = = = = =
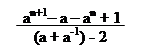
= = A.
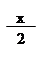 Обчислимо знаменник
Обчислимо знаменник
a + a-1 –2=cos x +isin x +cos x –isin x – 2 =2cos x – 2 = – 2(1 –cos x) = – 4 sin2;
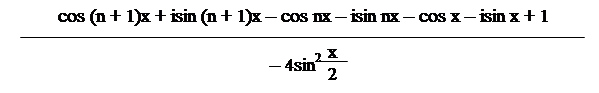 |
A = =
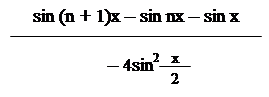 | |||
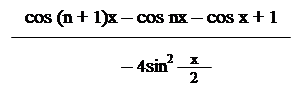 | |||
= + i;
Отже,
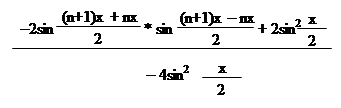 | |||
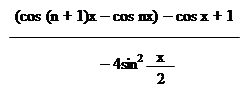 | |||
S = = =
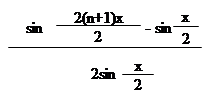
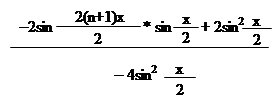 = = =
= = =
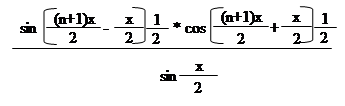 | 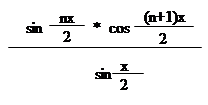 | ||
= =;
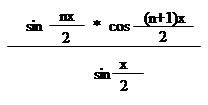 |
Відповідь:.
4. Знайти суму всіх первісних коренів 15-го степеня з одиниці.
Розв'язання: Нехай ξ1 – первісний корінь 15-го степеня з одиниці:
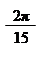 | |||
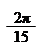 | |||
ξ1 = cos + isin;
Піднесенням ξ1 до степенів від 0 до 14 одержуємо всі корені 15-го степеня з одиниці. Сума всіх коренів 15-го степеня з одиниці дорівнює нулеві.
Знайдемо суму всіх первісних коренів 15-го степеня з одиниці. Позначимо її через S. Тоді
 |
S = Σ ξi – (1 + (ξ5 + ξ10) + (ξ3 + ξ6 + ξ9 + ξ12)) = 0 – (1 – 1 – 1) = 1.
Відповідь: S = 1.
5. Дана система лінійних неоднорідних рівнянь:
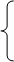 x1 – 2x2 + 3x3 = 2
x1 – 2x2 + 3x3 = 2
2x1 – x2 – 3x3 = –2
 x1 + 2x2 – 4x3 = –1
x1 + 2x2 – 4x3 = –1
 1 -2 3
1 -2 3
1. Знайти ранг матриці А = 2 -1 -3;
1 2 -4
2. Дослідити систему на сумісність.
3. Обчислити визначник матриці А способом
а) зведення до трикутного вигляду
б) розкладанням за елементами першого рядка
4. Розв'язати систему рівнянь методом Гауса, методом Крамера.
5. Знайти матрицю, обернену до матриці А двома способами.
6. Записати систему рівнянь в матричному вигдяді та розв'язати її в матричному вигляді.
Розв'язання:
1) Знайдемо ранг матриці А:
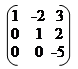
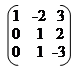
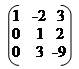
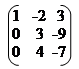
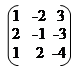 А = ~ ~ ~ ~; r(A) = 3.
А = ~ ~ ~ ~; r(A) = 3.
2) Досліджуємо систему рівнянь на сумісність за теоремою Кронекера-Капеллі. Виписуємо матрицю системи та розширену матрицю і знаходимо їх ранги.
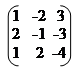 | 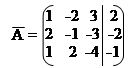 | ||
А =;.
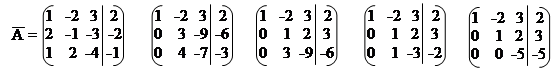 | |||
~ ~ ~ ~; r(A) = 3;
 r(A) = 3.
r(A) = 3.
 Отже, система рівнянь сумісна, так як ранг матриці А дорівнює рангу матриці А.
Отже, система рівнянь сумісна, так як ранг матриці А дорівнює рангу матриці А.
3) Обчислимо визначник матриці А:
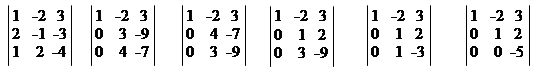 |
а)
| A | = = = – = – = –3 = –3 = 15
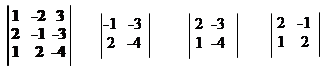 |
б)
| A | = = 1 + 2 + 3 = 10 + 2 * (-5) + 3 * 5 = 15.
4) Розв'яжемо систему рівнянь методом Гауса. Так як елементарні перетворення матриці не змінюють її рангу, а кожній матриці можна поставити у відповідність систему лінійних рівнянь, одержуємо:
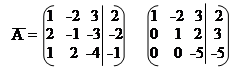
~.
 x1 – 2x2 + 3x3 = 2 x1 = 1;
x1 – 2x2 + 3x3 = 2 x1 = 1;
x2 + 2x3 = 3 ~ x2 = 1;
–5x3 = –5 x3 = 1;
Відповідь: (1, 1, 1).
Розв'яжемо систему рівнянь, застосовуючи формули Крамера:
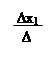 | 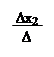 | 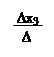 |
x1 =; x2 =; x3 =.
Так як визначник матриці відмінний від нуля, то система сумісна і має єдиний розв'язок.
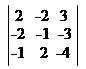 |
Знайдемо ∆x1 = = 8 – 12 – 6 – 3 + 12 + 16 = 15;
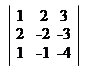 |
∆ = 15; ∆x2 = = 8 – 6 – 6 + 6 – 3 + 16 = 15;
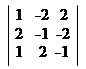 |
∆x3 = = 1 + 8 + 4 + 2 + 4 – 4 = 15;
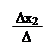 | 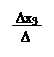 | ||||
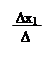 | |||||
x1 =; x1 = 1; x2=; x2 = 1; x3=; x3 = 1.
Відповідь: (1, 1, 1).
5) Знайдемо матрицю, обернену до матриці А. Матриця А невироджена (|А| ¹ 0), а тому має обернену.
а) Методом алгебраїчних доповнень знайдемо матрицю А*, приєднану до матриці А.
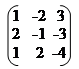 |
A11 = 10; A21 = –2; A31 = 9;
А =; A12 = 5; A22 = –7; A32 = 9;
A13 = 5; A23 = –4; A33 = 3.
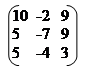 | |||
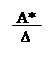 | |||
A* =. A-1 =; ∆ = 15.
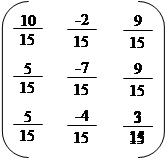 |
A-1 =.
б) Знайдемо обернену матрицю методом елементарних перетворень комбінованої матриці. Запишемо комбіновану матрицю:
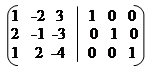 |
(А / Е) =
Зводимо цю матрицю до вигляду (Е / А-1).
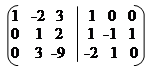
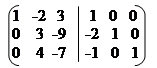
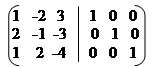
(А / Е) ~ ~ ~ ~
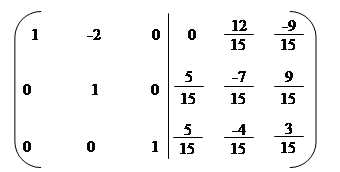 | |||
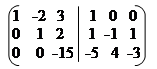 | |||
~ ~ ~
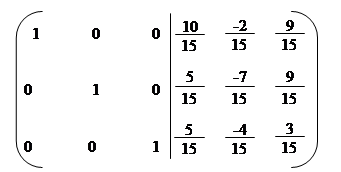 |
~
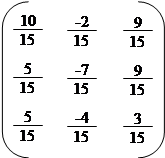 |
А-1 =.
6) Запишемо систему рівнянь у матричному вигляді:
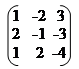 | 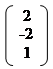 | 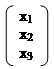 | |||||
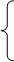 | |||||||
x1 – 2x2 + 3x3 = 2
2x1 – x2 – 3x3 = –2 А =; В =; Х =.
x1 + 2x2 – 4x3 = –1
Тоді система рівнянь приймає вид: А * Х = В або
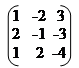 | 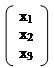 | 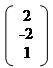 |
* =, звідси Х = А-1 * В – розв'язок системи.
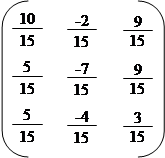 | |||
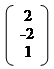 | |||
Х = * =
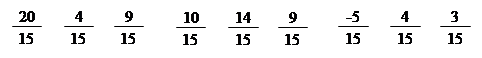 |
=(+ –; + –; + –) = (1, 1, 1).
Відповідь: Х = (1, 1, 1).
6. За допомогою теореми про накладання розв'язків знайти загальний розв'язок системи лінійних рівнянь:
 x1 + 2x2 + x3 + 3x4 = 9
x1 + 2x2 + x3 + 3x4 = 9
2x1 – x2 – 3x3 + x4 = –2
|
|
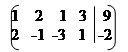 |
А =.
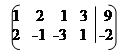 Знайдемо ранг матриці А:
Знайдемо ранг матриці А:
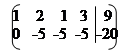 |
 ~; r(A) = 2; r(A) = 2.
~; r(A) = 2; r(A) = 2.
Так як ранг матриці системи дорівнює рангу розширеної матриці, то дана система сумісна і має безліч розв'язків (r < n), де n – кількість невідомих.
Дана система рівнянь еквівалентна системі:
|
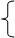 x1 + 2x2 + x3 + 3x4 = 9 x1 + 2x2 + x3 + 3x4 = 9
x1 + 2x2 + x3 + 3x4 = 9 x1 + 2x2 + x3 + 3x4 = 9 –5x2 – 5x3 – 5x4 = -20 x2 + x3 + x4 = 4
Нехай х3 і х4 – вільні невідомі. Надамо їм нульових значень: х3 = х4 = 0, тоді
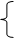
|
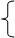 x1 + 2x2 = 9 х1 = 1;
x1 + 2x2 = 9 х1 = 1; x2 = 4 х2 = 4;
Отже, Х0 = (1, 4, 0, 0) – деякий частинний розв'язок заданої системи рівнянь.
Запишемо однорідну систему лінійних рівнянь, відповідну заданій системі:
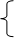 x1 + 2x2 +x3 + 3x4 = 0;
x1 + 2x2 +x3 + 3x4 = 0;
x2 + x3 + x4 = 0.
Знайдемо фундаментальну систему розв'язків цієї системи; вона складається з
4 – 2 = 2 розв'язків. У просторі R2 візьмемо базис: е1 = (1, 0); е2 = (0, 1) і вільним невідомим х3 і х4 надамо значень з базису <е1, е2>.
|
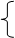
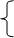 х3 = 1; х1 + 2х2 = –1; х1 = 1;
х3 = 1; х1 + 2х2 = –1; х1 = 1; х4 = 0; х2 = –1; х2 = –1,
|
тоді Х' = (-1, -1, 1, 0) – один із фундаментальних розв'язків однорідної системи.
Нехай х3 = 0, х4 = 1, тоді одержуємо:
|
 х3 = 0; х1 + 2х2 = –3; х1 = –1;
х3 = 0; х1 + 2х2 = –3; х1 = –1; х4 = 1; х2 = –1; х2 = –1
|
і вектор Х'' = (-1, -1, 0, 1) – другий фундаментальний розв'язок.
Загальний розв'язок однорідної системи знаходимо як лінійну комбінацію фундаментальних розв'язків:
|
|
| |||||||
| |||||||||
Х = αХ' + βХ''; Х = (α, -α, α, 0) + (-β, -β, 0, β) = (α – β, -α – β, α, β); α, β Є R.
Загальний розв'язок даної системи лінійних неоднорідних рівнянь має вигляд:
|
Х= Х0 + Х = (1, 4, 0, 0) + (α – β, -α – β, α, β) = (1 – α – β; 4 – α – β; α, β); α, β Є R.
Відповідь: (1 – α – β; 4 – α – β; α, β); α, β Є R.
Контрольна робота № 3
1. Перевірити чи утворюють наступні множини векторні простори над полем дійсних чисел R
1. Сукупність векторів площини, початок кожного з яких збігається з початком координат, а кінець міститься в першій або четвертій координатних четвертях;
2. Множина многочленів степеня 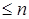 від однієї змінної дійсними коефіцієнтами;
від однієї змінної дійсними коефіцієнтами;
3. Множина всіх функцій, неперервних на відрізку 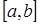
4. Множина всіх збіжних послідовностей;
5. Множина квадратних матриць порядку n відносно звичайних операцій додавання матриць і множення їх на число.
6. Множина всіх многочленів f (х), що задовольняють умові f(0)= 1 відносно додавання многочленів і множення їх на число;
7. Множина комплексних чисел (зокрема, розглянути множину над полем раціональних чисел відносно звичайних операцій додавання і множення їх на число);
8. Множина всіх функцій, інтегрованих на відрізку 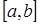 ;
;
9. Розв’язки довільної системи лінійних однорідних рівнянь над деяким полем  P.
P.
10. Множина P додатних чисел з наступними операціями: додавання - для будь-яких 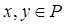 “х+у=ху”, множення на число з поля K0- для будь-яких
“х+у=ху”, множення на число з поля K0- для будь-яких 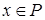 і
і 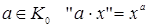 .
.
ІІ. Довести, що вектори 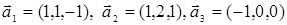 утворюють базис та знайти координати вектора
утворюють базис та знайти координати вектора 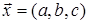 в цьому базисі.
в цьому базисі.
Таблиця параметрів:
 Варіант параметр Варіант параметр | ||||||||||
| a | -1 | -3 | -2 | -2 | ||||||
| b | -2 | -3 | -5 | |||||||
| c | -1 | -3 | -3 | -1 |
ІІІ. Довести, що кожна з двох даних систем векторів є базисом і знайти зв’язок між координатами того самого довільно вибраного вектора в цих двох базисах.
1. 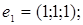
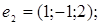
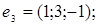
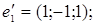
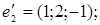
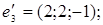
2. 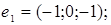
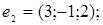
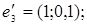
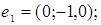
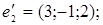
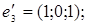
3. 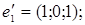
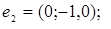
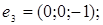
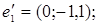
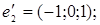
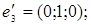
4. 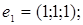
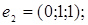
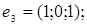
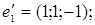
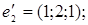
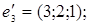
5. 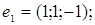
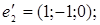
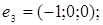
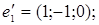
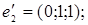
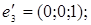
6. 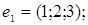
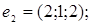
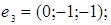
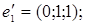
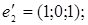
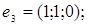
7 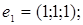
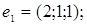
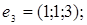
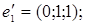
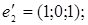
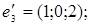
8. 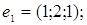
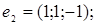
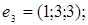
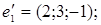
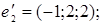
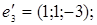
9. 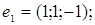
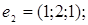
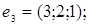
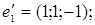
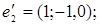
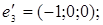
10. 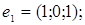
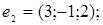
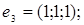
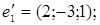
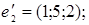
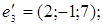
ІV. Знайти базиси суми і перетину векторних підпросторів V і U, заданих як лінійні оболонки векторів  a 1, a 2,... ak і b1, b2,….,b і відповідно.
a 1, a 2,... ak і b1, b2,….,b і відповідно.
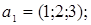
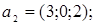
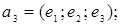
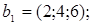
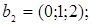
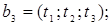
Таблиця параметрів
 Варіант параметр Варіант параметр | ||||||||||
| e1 | -2 | -4 | -5 | -2 | ||||||
| e2 | -2 | -2 | -2 | -4 | -7 | |||||
| e3 | -1 | -5 | -8 | -2 | ||||||
| t1 | -2 | -2 | -2 | -4 | -7 | |||||
| t2 | -3 | -2 | -5 | -9 | -2 | |||||
| t3 | -4 | -2 | -8 | -14 | -6 |
V. На вектори 
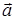 ,
, 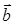 ,
, 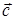 натягнута лінійна оболонка L
натягнута лінійна оболонка L
а) побудувати ортонормований базис простору L;
б) знайти ортогональне доповнення 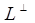 ;
;
в) знайти відповідно проекції 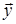 і
і 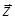 вектора
вектора 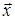 на підпростори
на підпростори 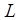 і
і 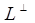
г) знайти кут між вектором 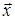 і простором
і простором 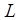 ;
;
д) знайти відстань між вектором 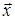 і підпростором
і підпростором 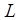 ;
;
Таблиця параметрів
 Варіант параметр Варіант параметр | ||||||||||
| а1 | ||||||||||
| а2 | -1 | |||||||||
| а3 | -2 | -1 | ||||||||
| а4 | -1 | -2 | -1 | -2 | -1 | -1 | ||||
| b1 | ||||||||||
| b2 | -5 | |||||||||
| b3 | -1 | -5 | -2 | |||||||
| b4 | -1 | -1 | -3 | -3 | ||||||
| c1 | ||||||||||
| c2 | -1 | |||||||||
| c3 | -1 | -1 | -6 | |||||||
| c4 | -1 | -7 | -4 | |||||||
| x1 | -1 | |||||||||
| x2 | -2 | -1 | -2 | -1 | ||||||
| x3 | -1 | -2 | -3 | -3 | -3 | -1 | -3 | |||
| x4 |



VІ. Довести, що множення кожної квадратичної матриці другого 
порядку з дійсними елементами зліва на матрицю 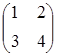 є лінійним оператором векторного простору квадратних матриць другого порядку над полем дійсних чисел R. Знайти матрицю цього лінійного оператора у базисі, що складається з матриць:
є лінійним оператором векторного простору квадратних матриць другого порядку над полем дійсних чисел R. Знайти матрицю цього лінійного оператора у базисі, що складається з матриць:
- E1 =
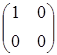 ;
; 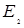 =
= 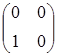 ;
; 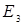 =
= 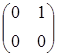 ;
; 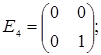
VІІ. Нехай лінійний оператор A в базисі а = < а1, а2 > має матрицю 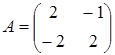 , а лінійний оператор B у базисі b=<b1,b2,> має матрицю
, а лінійний оператор B у базисі b=<b1,b2,> має матрицю 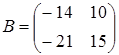 . Знайти матрицю Х лінійного оператора AB в базисі, в якому задано координати всіх векторів.
. Знайти матрицю Х лінійного оператора AB в базисі, в якому задано координати всіх векторів.
 Таблиця параметрів
Таблиця параметрів
| Варіант параметр | ||||||||||
| а1 | (-3,-1) | (1,3) | (1,-1) | (-1,2) | (2,3) | (1,7) | (2,-3) | (4,1) | (3,1) | (1,-4) |
| а2 | (7,2) | (2,5) | (7,2) | (3,1) | (1,5) | (5,2) | (1,2) | (5,3) | (-1,4) | (3,2) |
| б1 | (3,2) | (-1,2) | (1,3) | (2,-1) | (1,2) | (-1,3) | (1,1) | (-2,-1) | (1,5) | (2,1) |
| б2 | (4,3) | (3,2) | (4,2) | (1,1) | (3,4) | (2,3) | (2,0) | (3,4) | (3,2) | (-1,1) |
VІІІ. Побудувати ядро 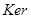 A область значень ImA, та знайти ранг r=dim(ImA), дефект d=dim(KerA) лінійного оператора A векторного простору L3, який у деякому базисі цього простору B=<
A область значень ImA, та знайти ранг r=dim(ImA), дефект d=dim(KerA) лінійного оператора A векторного простору L3, який у деякому базисі цього простору B=< 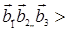 заданий своєю матрицею:
заданий своєю матрицею:
1. 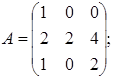 2.
2. 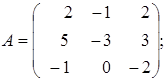 3.
3. 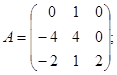
4. 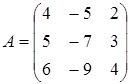 ; 5.A=
; 5.A= 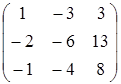 ; 6.
; 6. 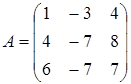
7.A= 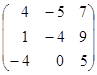 ; 8. A=
; 8. A= 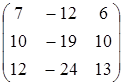 ; 9. A=
; 9. A= 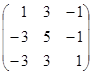 ;
;
10.A= 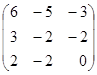 ;
;
IX. Знайти власні значення і власні вектори лінійного оператора A, заданого в деякому базисі B=<b1,b2,b3> цього простору матрицями n.VIII.
X. Чи зводиться відповідна матриця А n.VIII n. IX лінійного оператора A векторного простору V3 до діагонального виду за допомогою переходу до іншого базису? Знайти цей базис і відповідну йому матрицю.
Зразки розв’язання задач контрольної роботи № 3
І. Довести, що квадратні матриці порядку n з дійсними елементами утворюють векторний простір над полем дійсних чисел, якщо за операції взяти додавання матриць і множення матриці на число.
Розв’язання. Нехай М- множина всіх квадратних матриць порядку n з дійсними елементами.
 2015-07-14
2015-07-14 1590
1590