Дана окружность с центром в начале координат и радиусом 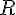 (рис. 3).
(рис. 3).

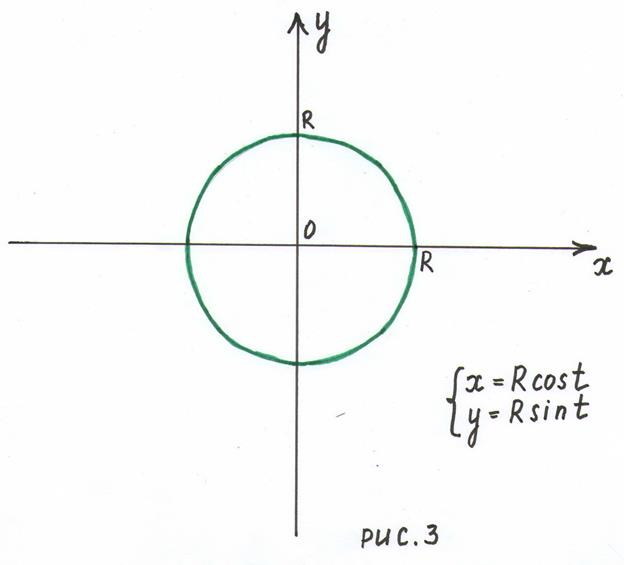
Пусть 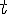 - это угол, образованный радиусом этой окружности, и осью
- это угол, образованный радиусом этой окружности, и осью 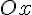 . Тогда координаты любой точки окружности выражаются через параметр
. Тогда координаты любой точки окружности выражаются через параметр 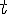 следующим образом:
следующим образом:
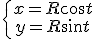
Причем 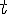 изменяется от 0 до
изменяется от 0 до 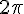 . Это и есть параметрическое уравнение окружности. Возводя в квадрат оба уравнения и складывая их, получаем каноническое уравнение окружности:
. Это и есть параметрическое уравнение окружности. Возводя в квадрат оба уравнения и складывая их, получаем каноническое уравнение окружности:
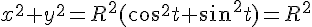 .
.
Для того чтобы найти производную функции, заданной в параметрическом виде, используется формула:
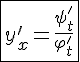 или
или 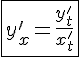 .
.
Для нахождения второй производной параметрической функции используется следующая формула:
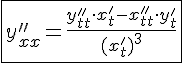 .
.
Пример. Функция задана параметрическим уравнением: 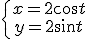
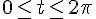 .
.
Найти производную функции 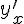 при любом значении параметра t и при
при любом значении параметра t и при 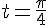 . Найти угловой коэффициент касательной в точке, соответствующей значению параметра
. Найти угловой коэффициент касательной в точке, соответствующей значению параметра 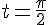 .
.
 2015-07-14
2015-07-14 706
706








