Теорема. Пусть функция  непрерывна на отрезке
непрерывна на отрезке 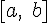 , дифференцируема на интервале
, дифференцируема на интервале 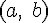 и принимает на концах отрезка равные значения
и принимает на концах отрезка равные значения 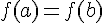 . Тогда существует по крайней мере одна точка
. Тогда существует по крайней мере одна точка 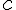 на интервале
на интервале 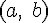 , для которой
, для которой 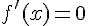 .
.
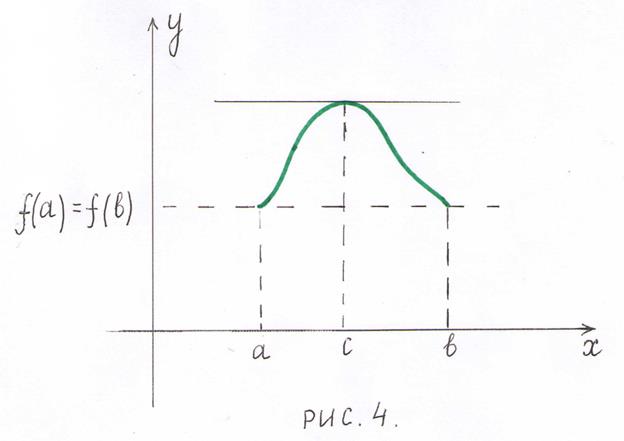
Геометрически теорема Ролля означает, что у графика непрерывной на отрезке 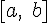 и дифференцируемой внутри него функции, принимающей на концах этого отрезка равные значения, существует хотя бы одна точка
и дифференцируемой внутри него функции, принимающей на концах этого отрезка равные значения, существует хотя бы одна точка 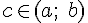 , в которой касательная параллельна оси абсцисс (рис.4).
, в которой касательная параллельна оси абсцисс (рис.4).
Пример 1. Необходимо проверить, справедлива ли терема Ролля для функции 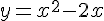 на отрезке
на отрезке 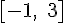 , и найти соответствующее значение
, и найти соответствующее значение 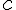 .
.
Решение. Функция непрерывна на этом отрезке и дифференцируема на интервале 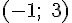 . Кроме того,
. Кроме того, 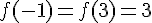 , поэтому теорема Ролля для данной функции на данном отрезке справедлива. Найдем значение
, поэтому теорема Ролля для данной функции на данном отрезке справедлива. Найдем значение 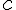 , для которого
, для которого 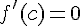 , из уравнения
, из уравнения 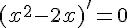 , то есть
, то есть 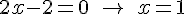 . Поскольку найденная точка принадлежит интервалу
. Поскольку найденная точка принадлежит интервалу 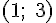 , то
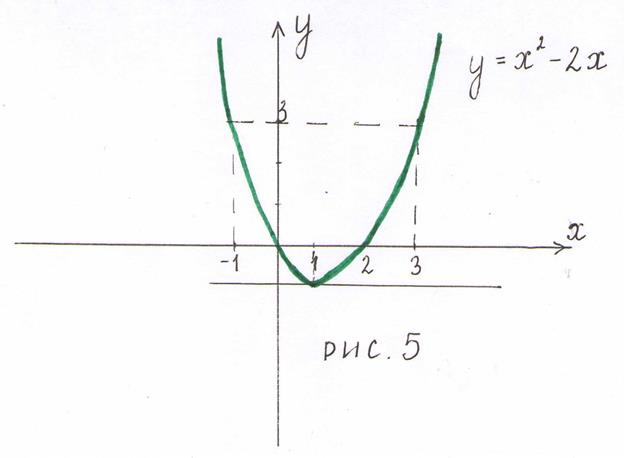
, то 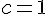 - искомое значение. Касательная, проведенная к графику функции в этой точке, параллельна оси абсцисс (рис.5).
- искомое значение. Касательная, проведенная к графику функции в этой точке, параллельна оси абсцисс (рис.5).
Пример 2. Проверить, справедлива ли теорема Ролля на отрезке 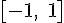 для функций
для функций 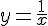 и
и 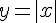 .
.
Решение. Функция 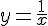 имеет точку разрыва в точке
имеет точку разрыва в точке 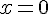 , принадлежащую заданному отрезку, поэтому на этом отрезке она не удовлетворяет теореме Ролля (рис.6).
, принадлежащую заданному отрезку, поэтому на этом отрезке она не удовлетворяет теореме Ролля (рис.6).
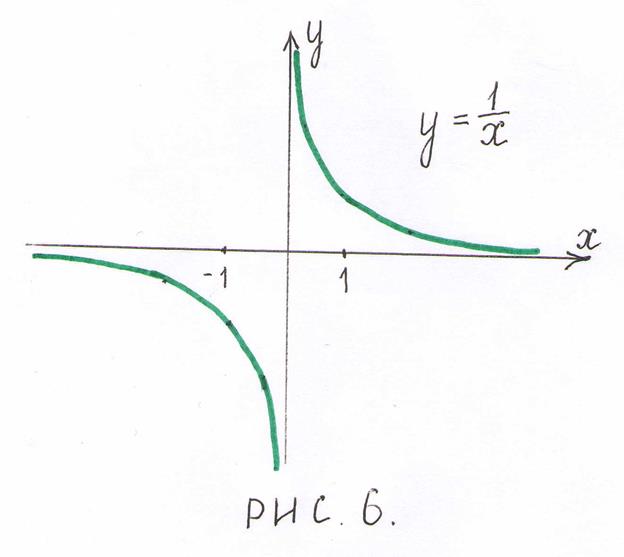
Рассмотрим на этом же отрезке функцию 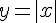 . Эта функция непрерывна на отрезке
. Эта функция непрерывна на отрезке 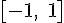 и принимает на концах отрезка равные значения, но в точке
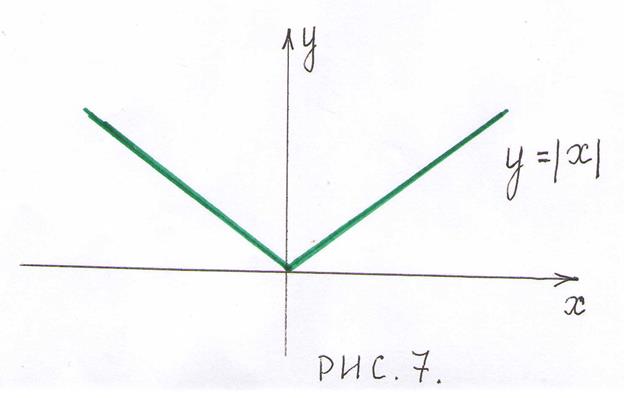
и принимает на концах отрезка равные значения, но в точке 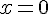 она не дифференцируема, поэтому она не удовлетворяет теореме Ролля на заданном отрезке (рис.7).
она не дифференцируема, поэтому она не удовлетворяет теореме Ролля на заданном отрезке (рис.7).
Вопрос. Какая функция удовлетворяет теореме Ролля на отрезке 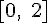 ?
?
Начало формы
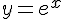 | |
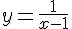 | |
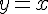 | |
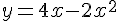 |
 2015-07-14
2015-07-14 2608
2608
