2015-07-14
8196
Теорема. Пусть функция непрерывна на отрезке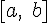 
и дифференцируема на интервале 
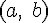. Тогда на интервале 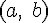найдется такая точка 
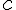, что
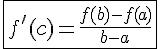
Выясним геометрический смысл теоремы Лагранжа. Величина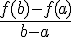 
есть угловой коэффициент прямой, проходящей через точки 
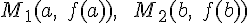, принадлежащие графику функции 
. Из теоремы Лагранжа следует, что существует такая точка 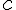такая, что касательная к графику функции в точке 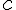параллельна данной прямой. Таких точек может быть несколько, но, по крайней мере, одна всегда существует (рис. 8).
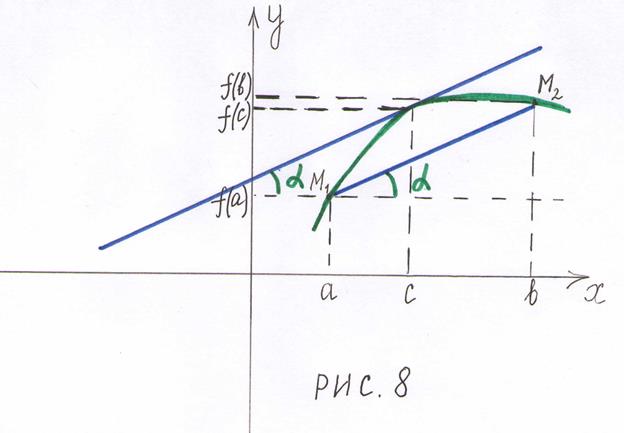
Пример 1. Проверить, что функция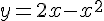 
удовлетворяет условиям теоремы Лагранжа на отрезке 
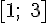, и найти точку .
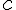Решение. Так как данная функция непрерывна на отрезке 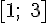и дифференцируема во всех внутренних точках этого отрезка, то она удовлетворяет условиям теоремы Лагранжа. Следовательно, внутри этого отрезка существует точка, удовлетворяющая равенству:
.
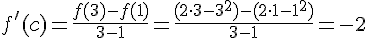Так как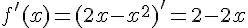 
, следовательно 
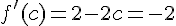, то есть 
.
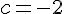Пусть функция удовлетворяет условиям теоремы Лагранжа на отрезке 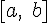, а точк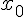и 
и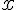 
принадлежат этому отрезку. Тогда функция удовлетворяет условиям теоремы Лагранжа на отрезке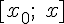 
и существует точка 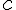, принадлежащая интервалу 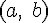, такая, что выполняется равенство
.
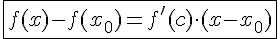Эта формула называется формулой конечных приращений Лагранжа.
Следствие 1. Если производная функции равна нулю на некотором промежутк е, то функция постоянна на этом промежутке.
Следствие 2. Если две функции имеют равные производные на некотором промежутке, то они отличаются друг от друга на постоянное слагаемое.
