Пусть функция  дифференцируема на некотором отрезке
дифференцируема на некотором отрезке 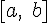 . Производная этой функции представляет собой также функцию от переменной
. Производная этой функции представляет собой также функцию от переменной 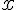 . Дифференцируя эту функцию, получаем вторую производную от функции
. Дифференцируя эту функцию, получаем вторую производную от функции  .
.
Производная от первой производной называется производной второго порядка или второй производной от первоначальной функции и обозначается символом 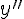 или
или 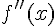 :
:
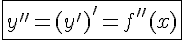 .
.
Выражение 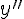 читается как "игрек два штриха".
читается как "игрек два штриха".
Так, например, если 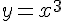 , то
, то 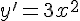 ,
, 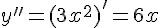 .
.
Производная от второй производной называется производной третьего порядка или третьей производной и обозначается 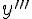 или
или 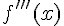 (читается "эф три штриха от икс").
(читается "эф три штриха от икс").
Производная от производной третьего порядка называется производной четвертого порядка или четвертой производной и так далее. Начиная с четвертой производные могут обозначаются римскими цифрами: 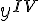 ,
, 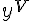 и т.д.
и т.д.
Производная 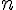 -порядка обозначается символом
-порядка обозначается символом 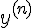 или
или 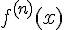 , а вычисляется по формуле
, а вычисляется по формуле
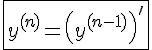
Правила дифференцирования производных высших порядков следующие:
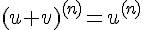 .
.
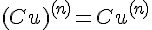 .
.
Пример: Вычислите производные 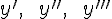 для функции
для функции 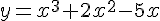 .
.
Решение: 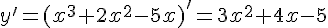 .
.
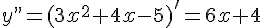
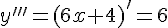 .
.
Вопрос. Производная четвертого порядка для функции 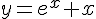 равна
равна
Начало формы
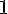 | |
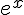 | |
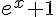 | |
 |
 2015-07-14
2015-07-14 2344
2344
