Теорема. Пусть функции 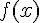 и
и 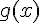 непрерывны на отрезке
непрерывны на отрезке 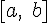 и дифференцируемы на интервале
и дифференцируемы на интервале 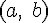 , причем
, причем 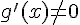 для всех
для всех 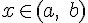 . Тогда найдется такая точка
. Тогда найдется такая точка 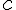 на этом интервале, что
на этом интервале, что
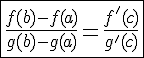 .
.
Эта формула называется формулой Коши или обобщенной формулой конечных приращений. Теорема Лагранжа является частным случаем теоремы Коши, если 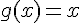 .
.
 2015-07-14
2015-07-14 1361
1361








