Правило Лопиталя – это простой и весьма эффективный способ раскрытия неопределенностей, используемый для вычисления пределов функций.
Следующая теорема дает правило раскрытия неопределенности вида 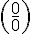 .
.
Теорема 1. Пусть функции 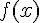 и
и 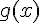 определены и дифференцируемы в окрестности точки
определены и дифференцируемы в окрестности точки 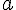 , за исключением, может быть, самой точки
, за исключением, может быть, самой точки 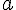 . Пусть также
. Пусть также 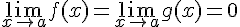 , где
, где 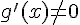 в указанной окрестности точки
в указанной окрестности точки 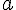 . Тогда, если существует предел отношения производных
. Тогда, если существует предел отношения производных 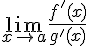 (конечный или бесконечный), то существует и предел
(конечный или бесконечный), то существует и предел 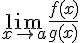 , причем справедлива формула:
, причем справедлива формула:
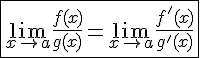 .
.
Пример 1. Найти предел, пользуясь правилом Лопиталя: 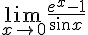 .
.
Решение. Функции 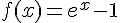 и
и 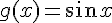 стремятся к нулю при
стремятся к нулю при 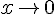 , причем
, причем 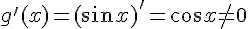 в окрестности точки
в окрестности точки 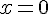 . Применяя правило Лопиталя, получим:
. Применяя правило Лопиталя, получим:
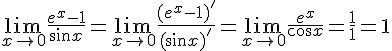
Вторая теорема Лопиталя позволяет раскрывать неопределенности вида 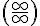 .
.
Теорема 2. Пусть функции определены и дифференцируемы в некоторой окрестности точки 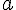 , за исключением, может быть, самой этой точки. Пусть
, за исключением, может быть, самой этой точки. Пусть 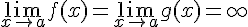 и
и 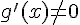 в окрестности точки
в окрестности точки 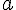 . Тогда, если существует предел отношения производных
. Тогда, если существует предел отношения производных 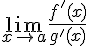 (конечный или бесконечный), то существует и предел
(конечный или бесконечный), то существует и предел 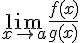 , причем справедлива формула
, причем справедлива формула
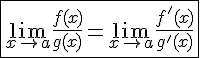 .
.
Если отношение 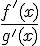 в свою очередь опять представляет собой неопределенность вида
в свою очередь опять представляет собой неопределенность вида 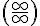 или
или 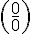 , то правило Лопиталя можно применять второй раз и т.д.
, то правило Лопиталя можно применять второй раз и т.д.
Пример 2. Найти предел, применяя правило Лопиталя: 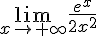 .
.
 2015-07-14
2015-07-14 1111
1111
