1. Відавочна, што тоесны аператар з’яўляецца самаспалучаным.
2. У V2 разгледзім аператар Prx праектавання на вось Ox. Відавочна, што 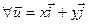
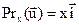 . Тады
. Тады 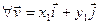
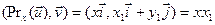 ,
, 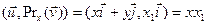 і
і 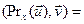
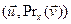 .
.
Такім чынам, даказалі, што Prx – самаспалучаны аператар.
Уласцівасць 18.2. Калі f – самаспалучаны аператар прасторы ε, U Ì ε - з’яўляецца f- інварыянтнай падпрасторай, тады артаганальнае дапаўненне да U
U 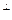
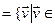 ε
ε 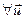 Î U
Î U 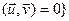
з’яўляецца f -інварыянтнай падпрасторай.
Доказ. Спачатку дакажам, што U 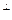 - падпрастора ў ε.
- падпрастора ў ε. 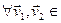 U
U 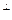 ,
, 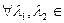 R,
R, 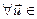 U
U 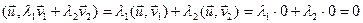 , значыцца,
, значыцца, 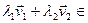 U
U 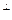 . Па крытэрыю падпрасторы з гэтага вынікае, што U
. Па крытэрыю падпрасторы з гэтага вынікае, што U 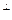 - падпрастора ў ε.
- падпрастора ў ε.
Паколькі 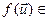 U,
U, 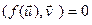 . З самаспалучанасці аператара f вынікае, што
. З самаспалучанасці аператара f вынікае, што 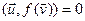 , значыцца
, значыцца 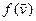 Î U
Î U 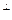 і U
і U 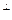 з’яўляецца f -інварыянтнай падпрасторай.n
з’яўляецца f -інварыянтнай падпрасторай.n
Уласцівасць 18.3. Калі f – самаспалучаны аператар прасторы ε, А – яго матрыца ў ортаўнармаваным базісе, тады А=АТ (1)
(нагадаем, што матрыцы, якія задавальняюць роўнасці (1) называюцца сіметрычнымі)
Доказ. Фіксуем адвольны ортаўнармаваны базіс у ε. Няхай у гэтым базісе f мае матрыцу А, адвольныя вектары 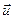 и
и 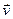 маюць слупкі каардынат X і Y. Тады вектары
маюць слупкі каардынат X і Y. Тады вектары 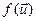 і
і 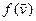 маюць слупкі каардынат AX і AY. Па уласцівасці 14.7
маюць слупкі каардынат AX і AY. Па уласцівасці 14.7
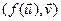 =(AX)T Y = X T A T Y, і
=(AX)T Y = X T A T Y, і 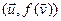 = X T AY.
= X T AY.
З самаспалучанасці f вынікае, што X T A T Y = X T AY. Так як X і Y – адвольныя слупкі, з апошняй роўнасці па леме 15.6 вынікае, што A T= A. n
Уласцівасць 18.4. Калі А – сіметрычная рэчаісная матрыца вымернасці n×n, тады для адвольнага ортаўнармаванага базіса ε n існуе лінейны самаспалучаны аператар f, які ў гэтым базісе мае матрыцу А.
Доказ. Існаванне лінейнага аператара f, які ў фіксаваным базісе мае матрыцу А, даказана ў уласцівасці 11.4. Дакажам, што f – самаспалучаны.
Калі 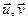 - адвольныя вектары з ε n маюць у дадзеным ортаўнармаваным базісе слупкі каардынат X і Y, тады, па пабудове аператара f, вектары
- адвольныя вектары з ε n маюць у дадзеным ортаўнармаваным базісе слупкі каардынат X і Y, тады, па пабудове аператара f, вектары 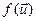 і
і 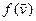 маюць у гэтым базісе слупкі каардынат AX і AY адпаведна.
маюць у гэтым базісе слупкі каардынат AX і AY адпаведна.
Па умове, базіс – ортаўнармаваны, значыцца можам выкарыстаць вынік 14.7:
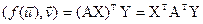 ;
; 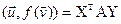 .
.
Паколькі матрыца А - сіметрычная, 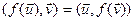 і аператар f – самаспалучаны.n
і аператар f – самаспалучаны.n
Уласцівасць 18.5. Калі 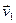 і
і 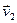 - уласныя вектары самаспалучанага аператара f, якім адпавядаюць няроўныя рэчаісныя ўласныя значэнні
- уласныя вектары самаспалучанага аператара f, якім адпавядаюць няроўныя рэчаісныя ўласныя значэнні 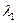 і
і 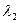 , тады вектары
, тады вектары 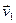 і
і 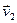 узаемаартаганальныя.
узаемаартаганальныя.
Доказ. Так як f – самаспалучаны аператар, 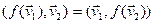 ,
, 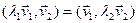 ,
, 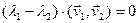 . Па умове
. Па умове 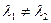 , значыцца,
, значыцца, 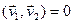 .n
.n
Лема 18.6. Калі f – лінейны аператар рэчаіснай лінейнай прасторы канечнай вымернасці n 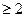 , тады існуе f -інварыянтная падпрастора U вымернасці 1 альбо 2.
, тады існуе f -інварыянтная падпрастора U вымернасці 1 альбо 2.
Доказ. Вядома, што кожны паліном з камплекснымі (у прыватнасці, з рэчаіснымі) каэфіцыентамі мае камплексны корань. Разгледзім характарыстычны паліном 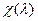 аператара f. Калі ён мае рэчаісны корань
аператара f. Калі ён мае рэчаісны корань 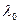 , тады, як даказана ў тэарэме 17.10, ён мае уласны вектар
, тады, як даказана ў тэарэме 17.10, ён мае уласны вектар 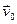 , якому адпавядае уласнае значэнне
, якому адпавядае уласнае значэнне 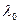 . Тады, відавочна, што прастора R
. Тады, відавочна, што прастора R 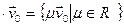 з’яўляецца f -інварыянтнай падпрасторай вымернасці 1.
з’яўляецца f -інварыянтнай падпрасторай вымернасці 1.
Няхай 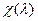 мае камплексны корань
мае камплексны корань 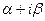 . Фіксуем у V некаторы базіс
. Фіксуем у V некаторы базіс 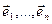 . Тады f мае ў гэтым базісе матрыцу А =(aij)n×n. Разгледзім сістэму адносна камплексных невядомых
. Тады f мае ў гэтым базісе матрыцу А =(aij)n×n. Разгледзім сістэму адносна камплексных невядомых 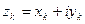 :.
:.
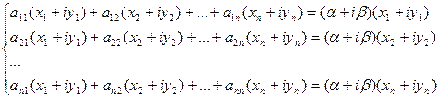 (2)
(2)
Калі ў сістэме (2) перанесці ўсе складнікі ў левую частку, атрымаем аднародную сістэму адносна невядомых 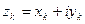 . Матрыца гэтай сістэмы будзе роўная A -
. Матрыца гэтай сістэмы будзе роўная A - 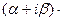 E, а яе дэтэрмінант роўны
E, а яе дэтэрмінант роўны 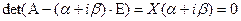 .
.
Атрымалі, што ранг аднароднай сістэмы меньшы за колькасць невядомых, значыцца сістэма мае ненулявое рашэнне 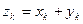 . Разгледзім два вектары з V:
. Разгледзім два вектары з V:
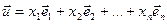 і
і 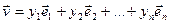 .
.
Перапішам сістэму (2), прыраўняўшы рэчаісныя і ўяўныя часткі камплексных лікаў: 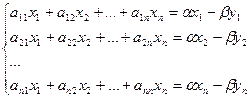 ;
; 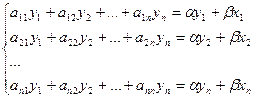 .
.
Апошнія дзве сістэмы перапішам ў матрычным выглядзе:
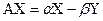 ,
, 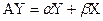 ,
,
што згодна з 11.5 эквівалентна таму, што 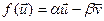 ,
, 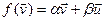 (3)
(3)
Разгледзім зараз падпрастору 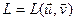 у V. З роўнасцей (3) вынікае, што
у V. З роўнасцей (3) вынікае, што 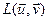 з’яўляецца f -інварыянтнай. Нескладана паказаць, што
з’яўляецца f -інварыянтнай. Нескладана паказаць, што 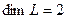 , але мы задаволімся тым, што
, але мы задаволімся тым, што 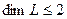 , чым закончым доказ лемы. n
, чым закончым доказ лемы. n
Уласцівасць 18.7. Усе уласныя лікі самаспалучанага аператара – рэчаісныя.
Доказ. Ад процілеглага. Няхай f мае уласны лік 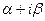 , дзе
, дзе 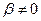 . З доказу лемы 18.6 вынікае, што існуюць ненулявыя вектары
. З доказу лемы 18.6 вынікае, што існуюць ненулявыя вектары 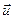 і
і 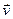 , якія задавальняюць роўнасцям (3). Тады
, якія задавальняюць роўнасцям (3). Тады
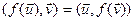 ;
; 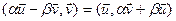 ;
; 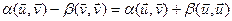 ;
;
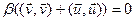 . Паколькі
. Паколькі 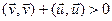 , атрымалі супярэчнасць.n
, атрымалі супярэчнасць.n
Тэарэма 18.8. Калі f – самаспалучаны аператар эўклідавай прасторы ε канечнай вымернасці, тады існуе ортаўнармаваны базіс, у якім f мае дыяганальную матрыцу.
Доказ. Выкарыстаем метад матэматычнай індукцыі па n=dim ε.
Калі n=1, тады адвольны лінейны аператар f ÎEnd(ε) мае выгляд 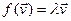 , ён будзе самаспалучаным і ў адвольным базісе мае матрыцу
, ён будзе самаспалучаным і ў адвольным базісе мае матрыцу 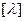 .
.
Няхай сцвярджэнне даказана, калі dim ε =n. Разгледзім выпадак, калі dim ε =n+1. Па 18.6 і 18.7 існуе уласнае рэчаіснае значэнне 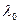 аператара f, якое адпавядае уласнаму вектару
аператара f, якое адпавядае уласнаму вектару 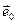 (можам лічыць, што
(можам лічыць, што 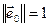 , паколькі можам пранармаваць ненулявы уласны вектар). Па уласцівасці 18.2, U – лінейная прастора вектароў, якія артаганальныя
, паколькі можам пранармаваць ненулявы уласны вектар). Па уласцівасці 18.2, U – лінейная прастора вектароў, якія артаганальныя 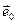 - з’яўляецца f -інварыянтнай прасторай (паколькі з’яўляецца артаганальным дапаўненнем да f -інварыянтнай прасторы
- з’яўляецца f -інварыянтнай прасторай (паколькі з’яўляецца артаганальным дапаўненнем да f -інварыянтнай прасторы 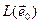 ).
).
Няхай dim U =k і 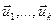 - базіс U. Разгледзім адвольны вектар
- базіс U. Разгледзім адвольны вектар 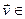 ε і дакажам, што ён раскладаецца па вектарам
ε і дакажам, што ён раскладаецца па вектарам 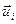 і вектару
і вектару 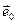 . Будзем шукаць такі рэчаісны лік
. Будзем шукаць такі рэчаісны лік 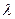 , каб вектары
, каб вектары 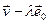 і
і 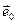 былі артаганальнымі:
былі артаганальнымі: 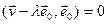 ;
; 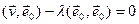 .
.
Паколькі 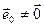 , тады
, тады 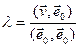 задавальняе ўмове.
задавальняе ўмове.
Такім чынам, 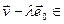 U, і раскладваецца па базісу:
U, і раскладваецца па базісу: 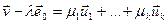 .
.
Адкуль вынікае патрэбны расклад 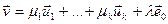 . Такім чынам, сістэма вектароў
. Такім чынам, сістэма вектароў 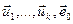 валодае ўласцівасцю паўнаты. Дакажам, што гэтыя вектары лінейна незалежныя. Няхай
валодае ўласцівасцю паўнаты. Дакажам, што гэтыя вектары лінейна незалежныя. Няхай 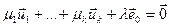 ,тады
,тады 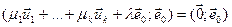 .
.
Паколькі 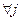
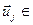 U,
U, 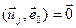 , маем, што
, маем, што 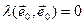 , а так як
, а так як 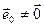 і
і 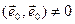 , значыцца
, значыцца 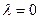 . Тады
. Тады 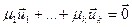 .Аднак,
.Аднак, 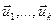 - базіс прасторы U, значыцца
- базіс прасторы U, значыцца 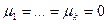 , чым даказана азначаная вышэй лінейная незалежнасць сістэмы вектароў
, чым даказана азначаная вышэй лінейная незалежнасць сістэмы вектароў 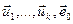 , з чаго вынікае, што яны ўтвараюць базіс ε, значыцца, k=n.
, з чаго вынікае, што яны ўтвараюць базіс ε, значыцца, k=n.
Так як падпрастора U з’яўляецца f -інварыянтнай, мы можам разгледзець f як самаспалучаны аператар прасторы U. Паколькі dim U =n, па пасылцы індукцыі існуе ортаўнармаваны базіс 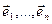 прасторы U, у якім f мае дыяганальную матрыцу
прасторы U, у якім f мае дыяганальную матрыцу 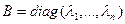 , прычым, з 17.2 вынікае, што
, прычым, з 17.2 вынікае, што 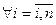
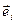 - уласныя вектары аператара f, якім адпавядаюць уласныя значэнні
- уласныя вектары аператара f, якім адпавядаюць уласныя значэнні 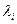 .
.
Атрымалі, што 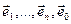 - ортаўнармаваны базіс прасторы ε. Значыцца,
- ортаўнармаваны базіс прасторы ε. Значыцца, 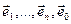 - ортаўнармаваны базіс прасторы ε, усе вектары яго з’яўляюцца ўласнымі вектарамі аператара f, і ў гэтым базісе f мае матрыцу A
- ортаўнармаваны базіс прасторы ε, усе вектары яго з’яўляюцца ўласнымі вектарамі аператара f, і ў гэтым базісе f мае матрыцу A 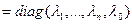 .n
.n
Уласцівасць 18.9. Для кожнай сіметрычнай матрыцы A ÎMat(n´n;R) існуе артаганальная матрыца Т такая, што матрыца T -1 AT - дыяганальная.
Доказ. Па ўласцівасці 18.4 можам лічыць, што А з’яўляецца матрыцай самаспалучанага аператара f у ортаўнармаваным базісе 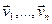 эўклідавай прасторы ε. Па ўласцівасці 18.8, існуе базіс
эўклідавай прасторы ε. Па ўласцівасці 18.8, існуе базіс 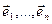 , у якім f мае матрыцу
, у якім f мае матрыцу 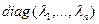 . Калі Т – матрыца пераходу ад першага базіса да другога, тады па тэарэме 11.8 T -1 AT
. Калі Т – матрыца пераходу ад першага базіса да другога, тады па тэарэме 11.8 T -1 AT 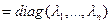 .n
.n
Вынік 18.10. Ва ўмовах уласцівасці 18.9 T T AT - дыяганальная.
Доказ. Паколькі матрыца Т артаганальная, T T= T -1.n
 2015-07-14
2015-07-14 587
587







