Определение

Функция 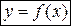называется дифференцируемой в точке 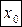, если ее приращение в этой точке:

,

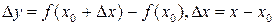представимо в виде:

,

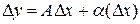где 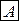- некоторое число, не зависящее от 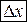, 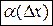- бесконечно малая более высокого порядка, чем 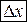, при .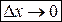

Линейная функция 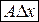называется дифференциалом функции 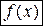в точке 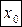и обозначается 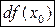, или, короче, .

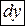Из определения производной следует, что:

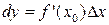или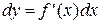

6. Свойства дифференциала.

Есл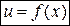и и 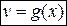- функции, дифференцируемые в точке 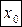, то из определения дифференциала следуют свойства:

1) ;

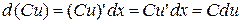2) ;

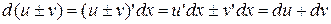3) ;

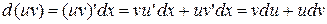4) ;

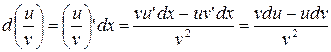7. Производная сложной функции.