Определение

Пусть функция 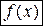определена в окрестности точки 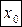и имеет в каждой точке этой окрестности производную 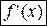. Если в точке 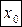существует производная функции 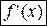, то она называется второй производной (производной второго порядка) функции 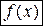и обозначается .

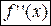Аналогично определяется производная порядка 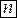при условии существования производной порядка :

.

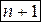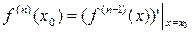Определение.

Значение дифференциала 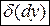, т.е дифференциала от первого дифференциала, в некоторой точке 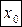при 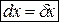называется вторым дифференциалом функции 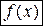в этой точке и обозначается :

.

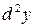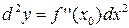Дифференциал порядка :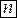

.

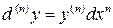11. Формула Тейлора.