Теорема. Производные и дифференциалы высших порядков

Пусть функция 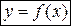непрерывна и строго монотонна в окрестности точки 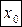, и в точке 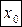существует производная 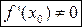. Тогда и обратная функция имеет производную в точке 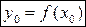, причем:

,

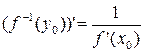т.е. производная обратной функции равна обратной величине производной данной функции.

10. Производные и дифференциалы высших порядков.