Теорема

Для того чтобы дифференцируемая на интервале 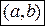функция 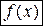возрастала (убывала) на этом интервале необходимо и достаточно, чтобы во всех его точках производная была неотрицательной, 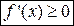(соответственно, неположительной, ).

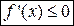Если всюду на 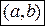производная положительна: 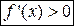(соответственно, отрицательна: 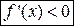), то функция 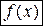строго возрастает (строго убывает) на рассматриваемом интервале.