Функция реализации

Тема 4. Принятие решений в условиях стохастической неопределенности (риска)

Функция реализации

Если предположить, что на результат принятия решений оказывает влияние некоторая среда, в которую погружена управляемая система, то всякую задачу принятия решения в условиях определенности, риска и неопределенности можно представить в форме функции реализа­ции.

Пусть, по-прежнему, задано множество всех альтернатив 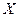и множество возможных исходов 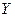. В общем случае ситуации принятия решений каждая альтернатива может привести к одному из нескольких возможных исходов. Какой именно исход реализуется, зависит от случайного параметра неопределенности 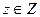. Будем считать, что неопределенность возникает из-за влияния на ситуацию внешних факторов, обусловленных состоянием среды в момент принятия решения. Тогда 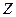представляет собой множество возможных состояний среды.

Каждый исход 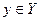, в силу сказанного, есть функция двух аргументов: 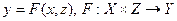, где 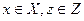. Будем называть F функцией реали­зации. Таким образом, функция реализации сопоставляет каж­дой паре вида (альтернатива, состояние среды) определяемый ею исход. Такую задачу при­нятия решения будем называть задачей принятия решения в форме функции реализации.

Если множество альтернатив и множество состояний среды конечны 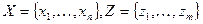, то ситуацию выбора альтернативы в условиях неопределенности можно представить с помощью матрицы 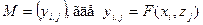, называемой матрицей решений.

Таблица 1. Матица решений

	Состояния среды
Альтернативы	z1	…	zj	…	zm
x1	y11	…	y1j	…	y1m
…	…		…		…
xi	yi1		yij		yim
…	…		…		…
xn	yn1		ynj		ynm

Заданная матрица интерпретируется следующим образом. Если выбрано решение 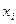, то может реализоваться любой исход из соответствующей строки матрицы: 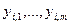. Какой именно исход будет реализован, зависит от состояния среды .

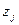Для описания задачи принятия решения в условиях определенности с помощью функции реализации, очевидно, необходимо ввести среду, име­ющую только одно состояние. Тогда можно построить матрицу решений, которая будет иметь только один столбец: в ее i -ю строку надо поместить исход, соответствующий альтерна­тиве .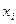

Задача принятия решения в условиях неопределенности отличается тем, что нельзя гарантировать наступление определенного исхода 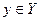при выборе некоторого решения 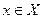. Следовательно, множество состояний среды 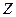должно состоять более чем из одного элемента.

Если каждому возможному состоянию сре­ды 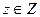, приписана вероятность его появления qj

,

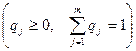то имеем задачу принятия решений в условиях стохастической неопределенности (риска).

Рассмотрим примеры ситуаций принятия решения в условиях неопределен­ности.

Пример 4.2 (зонтики, шляпы, плащи). Небольшое предприятие легкой промыш­ленности может выпускать продукцию одного из трех видов: зонтики, шляпы или плащи. Готовясь к летнему сезону, директор предприятия должен принять реше­ние — какой из этих трех видов продукции выпускать. При этом исход (доход предприятия) зависит от того, каким будет летний сезон — дождливым, жарким или умеренным. В дождливое лето наибольший доход принесет производство зонтиков, меньший — производство плащей и совсем малый — производство шляп. В жаркое лето наибольший доход даст производство шляп, средний — производ­ство зонтиков (которые можно использовать как от дождя, так и от солнца) и меньший — производство плащей. В умеренное лето наибольший доход от произ­водства плащей, несколько меньший — от производства шляп и еще меньший – от производства зонтиков. Пусть соответствующие доходы предприятия опреде­лены табл.4.3.

В данном примере принимающий решение может приписать вероятность каждому состоянию среды, если ему изве­стна статистика дождливых, жарких и умеренных лет (время года) в этой местности.

Таблица 4-3. Численные оценки доходов предприятия (функции реализации)

Альтернативы	Состояние среды
Дождливое лето	Жаркое лето	Умеренное лето
Производить зонтики
Производить шляпы
Производить плащи
Вероятности	0,6	0,1	0,3

Какое следует принять решение, если целью считать максимизацию дохода?

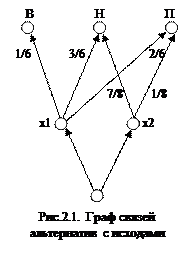
Пример 4.3 (о замене вратаря). Вернемся к задаче о замене вратаря на последних минутах хоккейного матча. Для наглядного представления задачи использовался граф связи альтернатив с исходами.

Здесь имеется:

две альтернативы: 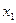– заменить вратаря, 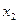– оставить вратаря;

три исхода: выигрыш (В), ничья (Н), поражение (П).

Приведенная формулировка задачи принятия решений в условиях риска легко отображается с помощью графа связей альтернатив с исходами (рис.2.1), но не позволяет понять, что является здесь состояниями среды и возможно ли, в этом случае, построить матрицу решений и функцию реализации.

Оказывается, язык функций реализации является достаточно универсальным языком и позволяет описывать подобные ситуации неопределенности.

Определим множество состоян ий среды, исходя из следующих рассуждений.

Знание состояния среды превращает ситуацию принятия решения в полностью определенную: выбор любой из альтернатив приводит к вполне определенному единственному исходу. Следовательно, на графе связей альтернатив с исходами каждому состоянию среды будет соответствовать свой подграф, в котором из каждой альтернативы 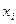исходит только одна дуга, указывающая, какой исход будет реализован при выборе этой альтернативы.

Обозначим 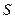– максимальное возможное число таких подграфов.

В качестве «состояний среды» возьмем множество всевозможных [«однозначных»] отображений 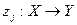, , 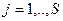удовле­творяющих тому условию, что 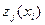есть исход, возможный при выборе альтернативы 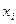(согласно графу связей альтернатив с исходами).

Выбор альтернативы 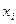и «состояния среды» 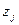, однозначно определяет исход – им является 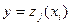, поэтому можно ввести функцию реали­зации F, определив ее условием .

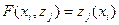Далее, каждому состоянию среды 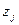припишем вероятность его наступления (вероятность реализации соответствующего подграфа)

, ,

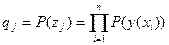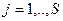где 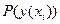– вероятность наступления исхода 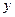, при выборе альтернативы 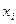в состоянии .

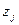Таким образом, для вычисления 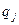нужно перемножить чис­ла, стоящие около дуг составляющих подграф, соответствующий отображению 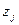. Теперь таблица, представляющая функцию реализации, может быть построена.

Следуя сказанному выше, в задаче о замене вратаря введем шесть искусственных «состояний среды»:

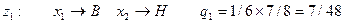
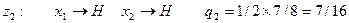
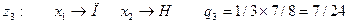
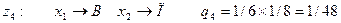
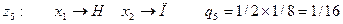
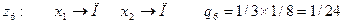
Теперь функция реализации может быть задана в виде таблицы (матрицы решений).

Таблица 4-3. Функция реализации (задача о замене вратаря)

Альтернативы	Состояния среды
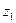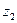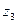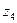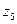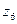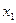	В	Н	П	В	Н	П
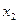	Н	Н	Н	П	П	П
Вероятности	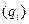7/48	7/16	7/24	1/48	1/16	1/24

Очевидно, что если мы имеем задачу принятия решения в условиях неопределенности, то приведение ее к форме функции реализации проводится аналогично, но, конечно, без нахождения вероятно­стей .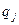

Установленная возможность представления всякой зада­чи принятия решения в форме функции реализации означает, что неопределенность, проявляющуюся в неоднозначной связи между средством и результатом, всегда можно объяснить существова­нием некоторой среды, оказывающей влияние на результат, причем условия определенности, риска и неопределенности при принятии решения будут определяться типом информированности принима­ющего решения о состоянии среды.

Методологическое же значение этого факта состоит в том, что широкий класс задач принятия решения приводится к некоторой стандартной форме – форме функции реализации.

Отметим, что многие практические задачи формулируются непосредственно в форме функции реализации. Это, прежде всего, задачи, где реально существует среда, влияющая на результат принятого решения. Например, задачи принятия оптимальных проектных решений в условиях технологического разброса параметров изделия.