Критерий математического ожидания

При наличии многократно реализованного исхода представляется разумным использование математического ожидания критерия в качестве оценки альтернативы :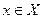

.

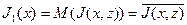Для расчета математи ческого ожидания случайной величины 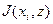бе­рется сумма произведений стоящих в строке xi табл.4.1 численных значений (оценок исходов) на соответствующие им вероятности:

оценка альтернативы xi есть .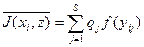

Концепция оптимальности решения: наилучшей (оптимальной) следует считать альтернативу, которой соответствует наибольшее значение математического ожидания.

Приведенное правило выбора оптимальной альтернативы называется критерием математического ожидания (или критерие м Байеса - Лапласа). Если предположить, что функция 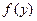характеризует «доход», полученный от реализовавшегося исхода 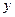, то математическое ожидание можно рассматривать как «средний доход», полученный на множестве реализаций, который мы и стремимся максимизировать.

В примере 4-2 предположим, что вероятности дождливого, жаркого и умерен­ного лета равны соответственно 0,6; 0,1; 0,3. Тогда оценки трех имеющихся альтернатив таковы:

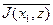= 0,6×90+0,1×60+0,3×40 = 72,

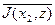= 0,6×25+0,1×100+0,3×50 = 40,

.

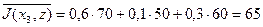В этом случае надо выбрать первую альтернативу.

В з адаче о замене вратаря будем численно оценивать исходы приносимыми ими очками: выигрыш оценивается в 2 очка, ничья – в 1 очко, проигрыш – 0.

Тогда при выборе альтернативы «заменить вратаря» математическое ожидание равно 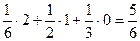, а при выборе альтернативы «оставить вратаря» 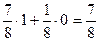. Таким образом, руководствуясь критерием числа «ожидаемых очков» надо отдать предпочтение второй альтернативе – «не заменять вратаря».