2015-07-14
437
В результате использования критерия математического ожидания Байеса-Лапласа мы получаем оценку каждого решения в виде ожидаемого среднего дохода на множестве реализовавшихся исходов. Однако каждый отдельно взятый исход будет давать разброс доходов относительно среднего значения, анализ которого позволяет оценить обусловленный неопределенностью риск принимаемого решения.
Возможный подход к оценке риска заключается в вычислении дисперсии и стандартного отклонения, как это делается для любого вида распределений.
Дисперсия случайной критериальной функции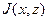 
вычисляется по обычной формуле:
.
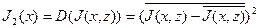Таким образом, можно сформулировать двухкритериальную задачу оптимизации, используя критерии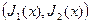 
, причем оценка дисперсии должна быть по возможности минимизирована.
Можно поступить и иначе. Как и в любой многокритериальной задаче можно осуществить свертку критериев, сформировав интегральный критерий с весовыми коэффициентами:
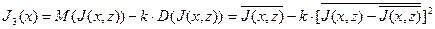, где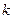 
– весовой коэффициент.
Коэффициент 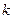целесообразно интерпретировать как степень несклонности к риску. Действительно, 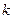определяет степень важности дисперсии по отношению к математическому ожиданию случайной величины 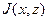. Увеличение значения 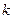приводит к уменьшению «среднего дохода», но зато уменьшается и величина отклонения от него. Таким образом, чем больше коэффициент 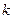, тем менее склонно к риску лицо, принимающее решение.
Если вернуться к примеру 4-2 и построить аддитивный критерий с весовыми коэффициентами, то результатом принятия решения с учетом риска обусловленного разбросом оценок исходов будет производство плащей, а не зонтиков, как было при использовании критерия математического ожидания.
Таблица 4-4. К
| Альтернативы | Состояние среды | Аддитивный критерий при различных k | ||||||
| Дождливое лето | Жаркое лето | Умеренное лето | M | D | 0,1 | 0,5 | ||
| Производить зонтики | 20,4 | -186 | -444 | |||||
| Производить шляпы | -12,5 | -222,5 | -485 | |||||
| Производить плащи | 60,5 | 42,5 | ||||||
| Вероятности | 0,6 | 0,1 | 0,3 |
Недостаток критерия: невозможно определить, каким должен быть коэффициент 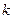для конкретного ЛПР в каждом конкретном случае. Метод не предусматривает процедуры выбора этого коэффициента.
Таким образом, в случае многократной реализации исхода принятого решения проблема выбора мало чем отличается (* может быть приведена*) от ситуаций, в которых случайные факторы отсутствуют. Дополнительные сложности здесь носят чисто вычислительный характер и связаны с необходимостью выполнения операции усреднения.
