Задача принятия решения в форме функции реализации как оптимизацонная

Пусть задана функция реализации 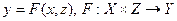, где множества 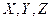не обязательно конечны.

Будем считать, что задана также функция 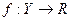, отображающая множество исходов 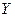на множество вещественных чисел 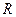и являющаяся оценкой исходов. Тогда существует функционал 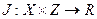и задача ПР становится эквивалентна задаче оптимизации

.

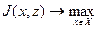Таким образом, здесь использован критериальный язык для описания отношения предпочтения на множестве исходов 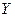. Исходы оцениваются по однокритериальной схеме в условиях, когда целевая функция задана не совсем точно – она содержит случайный параметр 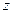. При наличии стохастической неопределенности предполагается, что 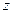– случайная величина, закон распределения которой известен.

Методологически важно различать две ситуации:

· Исход 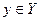, соответствующий принятому решению 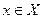, реализуется многократно.

· Исход 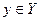реализуется однократно.

Например, выбор конструктивных параметров изделия, выпускаемого серийно, дает пример многократной реализации исхода одного и того же выбора. Напротив, оптимальный выбор параметров уникальных изделий (мостов, ирригационных сооружений, финансовых проектов, программных продуктов и т.п.) – пример второй ситуации.