Пусть функция 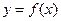 определена в промежутке
определена в промежутке 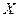 . Исходя из некоторого значения
. Исходя из некоторого значения 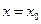 независимой переменной, придадим ему приращение
независимой переменной, придадим ему приращение  (
(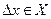 ), так что и новое значение
), так что и новое значение 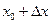 принадлежит промежутку
принадлежит промежутку 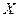 . Тогда значение
. Тогда значение 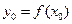 функции заменится новым значением
функции заменится новым значением 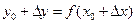 , то есть получит приращение
, то есть получит приращение
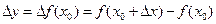
Если существует предел отношения приращения функции 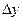 к приращению независимой переменной
к приращению независимой переменной  , при стремлении
, при стремлении  к нулю, то есть
к нулю, то есть
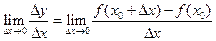 ,
,
то он называется производной функции 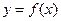 по независимой переменной
по независимой переменной 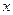 при данном её значении (или в данной точке)
при данном её значении (или в данной точке) 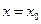 .
.
Задача о проведении касательной к кривой. Пусть дама кривая (K) (рис. 1) и на ней точка М; обратимся к установлению самого понятия касательной к кривой в ее точке М.
В школьном курсе касательную к окружности определяют как «прямую, имеющую с кривой лишь одну общую точку». Но это определение имеет частный характер, не вскрывая существа дела. Если попытаться применить его, например, к параболе
у = ах2 (рис. 2, а), то в начале координат О обе координатные оси подошли бы под это определение; на самом деле лишь ось х служит касательной к параболе в точке О!
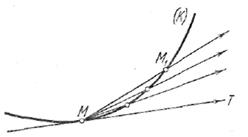
Рис.1
Мы дадим сейчас общее определение касательной. Возьмем на кривой (К) (рис. 1), кроме точки М, еще точку М1 и проведем секущую ММ1. Когда точка М1 вдоль по кривой будет перемещаться, эта секущая будет вращаться вокруг точки М.
Касательной к кривой (К) в точке М называется предельное положение МТ секущей ММ1, когда точка М1 вдоль по кривой стремится к совпадению с М. Смысл этого определения состоит в том, что угол М1МТ стремится к нулю, лишь только к нулю стремится хорда ММ1.
Применим для примера это определение к параболе y = a 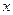 2 в произвольной ее точке М (
2 в произвольной ее точке М (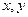 ). Так как касательная проходит через эту точку, то для уточнения ее положения достаточно знать еще ее угловой коэффициент. Мы и поставим себе задачей
). Так как касательная проходит через эту точку, то для уточнения ее положения достаточно знать еще ее угловой коэффициент. Мы и поставим себе задачей
найти угловой коэффициент  касательной в точке М
касательной в точке М
Придав абсциссе 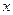 приращение
приращение  , от точки М кривой перейдём к точке
, от точки М кривой перейдём к точке
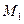 с абсциссой
с абсциссой 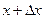 и ординатой
и ординатой 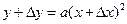 (рис. 2, а).
(рис. 2, а).
Угловой коэффициент 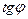 секущей
секущей 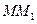 определится из прямоугольного треугольника
определится из прямоугольного треугольника
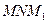 . В нём катет
. В нём катет 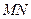 равен приращению абсциссы
равен приращению абсциссы  , а катет
, а катет 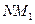 есть соответствующее приращение ординаты
есть соответствующее приращение ординаты 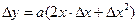 так что
так что
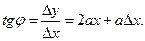
Для получения углового коэффициента касательной нужно перейти к пределу при 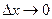 , так как это равносильно тому, что хорда
, так как это равносильно тому, что хорда 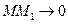 . При этом
. При этом 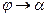 и
и 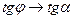 . Таким образом
. Таким образом
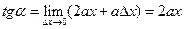 .
.
В случае любой кривой с уравнением
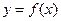
Угловой коэффициент касательной устанавливается подобным образом.
Приращению  абсциссы отвечает приращение
абсциссы отвечает приращение 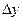 ординаты, и отношение
ординаты, и отношение
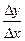
выражает угловой коэффициент секущей, 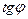 . Угловой же коэффициент
. Угловой же коэффициент
касательной получается отсюда путём перехода к пределу при 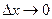 , то есть
, то есть
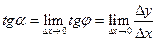 (рис 2,б)
(рис 2,б)
Угловой коэффициент  касательной есть производная от ординаты
касательной есть производная от ординаты
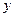 по абсциссе
по абсциссе 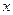
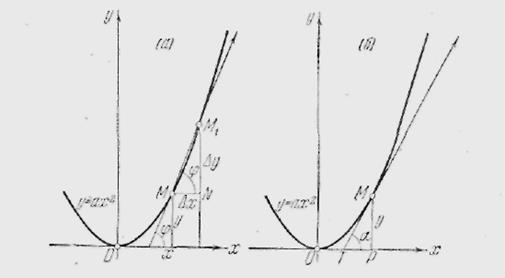
Рис. 2.
Процесс отыскания производной от данной функции называется дифференцированием этой функции
Если 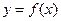 , то производную обозначают через
, то производную обозначают через 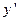 или
или 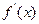 .
.

СВОДКА ФОРМУЛ ДЛЯ ПРОИЗВОДНЫХ 

Замечание. В формулах 18-20 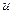 и
и 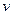 являются функциями от
являются функциями от 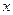 .
.
Приложения производной
- Возрастание и убывание функций
Известно, что функция 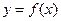 называется возрастающей на некотором интервале, если для любых двух значениях
называется возрастающей на некотором интервале, если для любых двух значениях 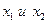 из указанного интервала неравенство
из указанного интервала неравенство 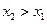
влечёт неравенство 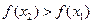 .
.
Если же для любых двух значениях 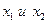 из указанного интервала неравенство
из указанного интервала неравенство 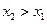
влечёт неравенство 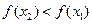 , то функция
, то функция 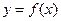 называется убывающей.
называется убывающей.
Рассмотрим функцию 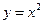 . Производная этой функции т. е
. Производная этой функции т. е 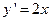 . Там где
. Там где 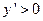 т.е
т.е
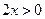 функцию
функцию 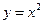 возрастает, а там где
возрастает, а там где 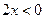 она убывает.
она убывает.
Таким образом мы видим, что возрастание и убывание функции тесным образом связаны со знаком производной.
Пусть дана функция 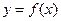 . Рассмотрим график этой функции(рис.3). Мы видим, что на интервале
. Рассмотрим график этой функции(рис.3). Мы видим, что на интервале 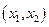 функция возрастает, на интервале
функция возрастает, на интервале 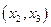 функция убывает.
функция убывает.
Далее на интервале 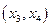 функция снова возрастает, а на интервале
функция снова возрастает, а на интервале 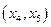 функция убывает и т. д. На интервалах возрастания функции касательная к кривой в каждой её точке образует с положительным направлением оси абсцисс острый угол, значит угловой коэффициент касательной (тангенс угла наклона касательной к положительному направлению оси абсцисс) есть число положительное. Отсюда в свою очередь следует,
функция убывает и т. д. На интервалах возрастания функции касательная к кривой в каждой её точке образует с положительным направлением оси абсцисс острый угол, значит угловой коэффициент касательной (тангенс угла наклона касательной к положительному направлению оси абсцисс) есть число положительное. Отсюда в свою очередь следует,
что производная вo всех точках указанного интервала будет положительной. Аналогично на интервалах убывания функции производная во всех точках будет отрицательной.
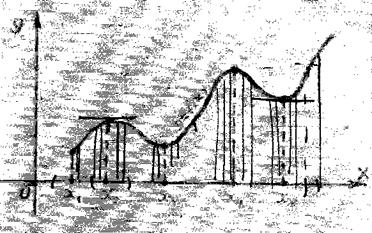
Рис. 3.
Рассмотрим теперь обратную задачу. Пусть при всех значениях 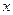 из некоторого интервала производная положительная. Имея ввиду, что производная в точке есть угловой коэффициент касательной к кривой (графику функции) в этой точке, и, учитывая, что производная положительная, можно заключить, что касательные образуют с положительным направлением оси абсцисс острый угол (рис. 4). Таким образом, график в данном интервале поднимается, следовательно, функция возрастает.
из некоторого интервала производная положительная. Имея ввиду, что производная в точке есть угловой коэффициент касательной к кривой (графику функции) в этой точке, и, учитывая, что производная положительная, можно заключить, что касательные образуют с положительным направлением оси абсцисс острый угол (рис. 4). Таким образом, график в данном интервале поднимается, следовательно, функция возрастает.
Пусть при всех значениях 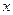 из некоторого интервала производная отрицательная, тогда, очевидно, можно заключить, что касательные образуют с положительным направлением оси абсцисс тупой угол (рис.4). Таким образом, график в этом интервале опускается, следовательно, функция убывает.
из некоторого интервала производная отрицательная, тогда, очевидно, можно заключить, что касательные образуют с положительным направлением оси абсцисс тупой угол (рис.4). Таким образом, график в этом интервале опускается, следовательно, функция убывает.
Отсюда можно сформулировать признак возрастания и убывания функции: если производная данной функции при всех значениях х на некотором интервале положительная, то функция на этом интервале возрастает, если же производная отрицательная, то функция убывает.
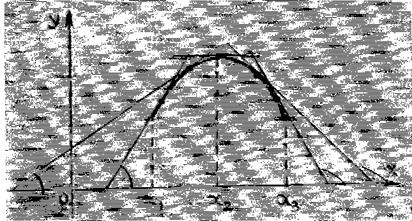
Рис. 4.
Отсюда правило: чтобы найти интервалы возрастания и убывания функции 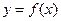 , надо найти производную и решить неравенства
, надо найти производную и решить неравенства 
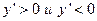 . Значения
. Значения 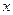 , при которых
, при которых 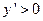 , дадут интервалы возрастания, значения
, дадут интервалы возрастания, значения 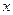 , при которых
, при которых 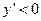 , дадут интервалы убывания.
, дадут интервалы убывания.
- Максимумы и минимумы функции
Рассматривая ход изменения функции 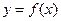 . (рис. 3), мы видим, что в точках
. (рис. 3), мы видим, что в точках 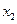 и
и 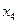 ординаты этой функции достигают наибольшего значения, а в точках
ординаты этой функции достигают наибольшего значения, а в точках 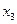 и
и 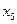 , наименьшего значения по сравнению со значениями ординат ближайших к ним точек. Такие точки называют соответственно точками максимума и точками минимума, а значения функции в этих точках соответственно максимумами и минимумами функции. Заметим, что в точках максимума возрастание сменяется убыванием, а в точках минимума, напротив, убывание сменяется возрастанием.
, наименьшего значения по сравнению со значениями ординат ближайших к ним точек. Такие точки называют соответственно точками максимума и точками минимума, а значения функции в этих точках соответственно максимумами и минимумами функции. Заметим, что в точках максимума возрастание сменяется убыванием, а в точках минимума, напротив, убывание сменяется возрастанием.
Итак, точка 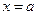 называется точкой максимума функции
называется точкой максимума функции 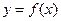 ., если значение функции в этой точке больше значений этой функции во всех точках, достаточно близких к а аналогично точка
., если значение функции в этой точке больше значений этой функции во всех точках, достаточно близких к а аналогично точка 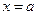 называется точкой минимума, если значение функции в этой точке меньше значений этой функции во всех точках, достаточно близких к а.
называется точкой минимума, если значение функции в этой точке меньше значений этой функции во всех точках, достаточно близких к а.
Локальный характер этих определений является очевидным (рис. 4). В самом деле, 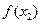 — максимум, a
— максимум, a 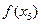 — минимум, тем не менее
— минимум, тем не менее 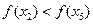 .
.
Пусть функция 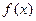 во всех точках некоторого интервала имеет производную
во всех точках некоторого интервала имеет производную 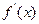 . Это значит, что график этой функции в каждой точке имеет определенную касательную, непа раллельную оси ординат. Предположим, что в точке
. Это значит, что график этой функции в каждой точке имеет определенную касательную, непа раллельную оси ординат. Предположим, что в точке 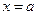 рассматриваемого интервала функция имеет максимум или минимум (для определенности положим максимум). Так как
рассматриваемого интервала функция имеет максимум или минимум (для определенности положим максимум). Так как 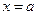 точка максимума, то слева, в достаточной близости к aфункция возрастает, т. е. производная положительная, а справа, в достаточной близости к aфункция убывает, т. е. производная отрицательная. Предполагая, что функция и ее производная изменяются без скачков, легко сделать вывод: в точках максимума функции производная равна нулю. Аналогичное заключение делаем и относительно точек минимума Итак, в точках максимума и минимума функции производная равна нулю. Это утверждение есть необходимый признак максимума и минимума функции. Оно не является достаточным признаком. В самом деле, производная функции
точка максимума, то слева, в достаточной близости к aфункция возрастает, т. е. производная положительная, а справа, в достаточной близости к aфункция убывает, т. е. производная отрицательная. Предполагая, что функция и ее производная изменяются без скачков, легко сделать вывод: в точках максимума функции производная равна нулю. Аналогичное заключение делаем и относительно точек минимума Итак, в точках максимума и минимума функции производная равна нулю. Это утверждение есть необходимый признак максимума и минимума функции. Оно не является достаточным признаком. В самом деле, производная функции 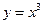 в точке
в точке 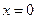 обращается в нуль, однако эта точка не является ни точкой максимума, ни точкой минимума.
обращается в нуль, однако эта точка не является ни точкой максимума, ни точкой минимума.
Значения 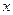 , при которых производная данной функции обращается в нуль, называются критическими значениями или просто критическими точками. В этих точках данная функция может иметь максимум или минимум, но может и не иметь. Таким образом, обращение производной данной функции в некоторой точке в нуль не может окончательно гарантировать наличие максимума или минимума в точке. Вопрос о максимуме и минимуме решается достаточным признаком, в основе которого лежат следующие две теоремы:
, при которых производная данной функции обращается в нуль, называются критическими значениями или просто критическими точками. В этих точках данная функция может иметь максимум или минимум, но может и не иметь. Таким образом, обращение производной данной функции в некоторой точке в нуль не может окончательно гарантировать наличие максимума или минимума в точке. Вопрос о максимуме и минимуме решается достаточным признаком, в основе которого лежат следующие две теоремы:
Теорема 1. Если для функции 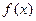 производная при
производная при 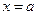 обращается в нуль, и если при переходе аргумента через
обращается в нуль, и если при переходе аргумента через 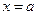 производная меняет знак плюс на минус, то
производная меняет знак плюс на минус, то 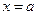 -точка максимума.
-точка максимума.
Теорема 2. Если для функции 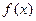 производная при
производная при 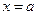 обращается в нуль, и если при переходе аргумента через
обращается в нуль, и если при переходе аргумента через 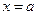 производная меняет знак минус на плюс то
производная меняет знак минус на плюс то 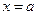 -точка минимума
-точка минимума
Таким образом, признак максимума и минимума будет следующий: Если для функции производная при х=а обращается в нуль и если при переходе аргумента через точку 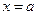 производная меняет знак, то
производная меняет знак, то 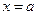 будет точкой максимума или минимума, причем будет точкой максимума, если производная знак плюс меняет на минус, и минимума, если производная знак минус меняет на плюс.
будет точкой максимума или минимума, причем будет точкой максимума, если производная знак плюс меняет на минус, и минимума, если производная знак минус меняет на плюс.
Отсюда получаем правило. Чтобы найти максимум или
минимум функции 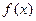 надо:
надо:
а) найти ее производную 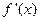
б) решить уравнение 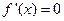 , отыскать действительные корни этого уравнения:
, отыскать действительные корни этого уравнения: 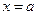 и др. (т. е. найти критические точки);
и др. (т. е. найти критические точки);
в) исследовать опрос о смене знака производной при переходе аргумента 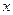 через данное исследуемое значение а и др. Пусть а — один из корней уравнения
через данное исследуемое значение а и др. Пусть а — один из корней уравнения 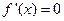
Тогда устанавливают знак производной во всех достаточно близких точках слева и справа от а.При этом нередко на практике, для простоты расхождений, берут в достаточной близости от адва значения 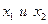 , где
, где 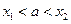 вычисляют производную в этих точках. Если
вычисляют производную в этих точках. Если 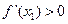
a 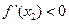 то заключают, что а - точка максимума. Если
то заключают, что а - точка максимума. Если 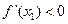
a 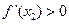 то заключают, что а - точка минимума.
то заключают, что а - точка минимума.
Если же 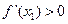 a
a 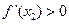 , или наоборот, то заключают, что при
, или наоборот, то заключают, что при 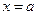
 2015-07-14
2015-07-14 743
743







