Дифференциалы высших порядков

Обозначение: d²y=d(dy).

При вычислении второго дифференциала учтем, что dx не зависит от х и при дифференцировании выносится за знак производной как постоянный множитель.

Итак,

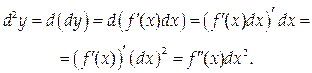
Подобным же образом можно найти третий дифференциал от данной функции:

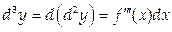
и дифференциалы более высоких порядков.

Дифференциалом n -го порядка называется первый дифференциал от дифференциала (n -1)-го порядка:

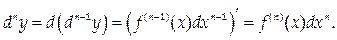
Свойства дифференциалов высших порядков

1. Производную любого порядка можно представить как отношение дифференциалов соответствующего порядка:

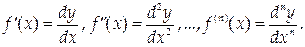
2. Дифференциалы высших порядков не обладают свойством инвариантности.

Покажем это на примере второго дифференциала. Если y=F(j(x))=F(u), где u=j(x), то d²y=d(F΄(u)du). Но du=j΄(x)dx зависит от х, поэтому

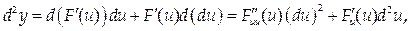
где

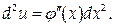
Таким образом, форма второго дифференциала изменилась при переходе к аргументу u.