Определение 23.4. Прямая называется асимптотой графика функции y = f(x), если расстояние от переменой точки этого графика до прямой стремится к нулю при удалении точки в бесконечность.
Рассмотрим три вида асимптот и определим способы их нахождения.
1. Вертикальные асимптоты – прямые, задаваемые уравнениями вида х = а. В этом случае определение асимптоты подтверждается, если хотя бы один из односторонних пределов функции в точке а бесконечен.
Пример. Вертикальной асимптотой графика функции
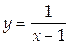
является прямая х = 1.
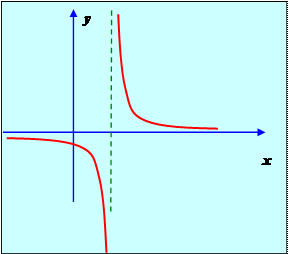
Рис. 5
2. Горизонтальные асимптоты – прямые вида у = а. Такие асимптоты имеет график функции, предел которой при 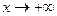 или при
или при 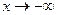 конечен, т.е.
конечен, т.е.
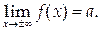
Пример. Горизонтальными асимптотами функции y = arctg x являются
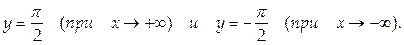
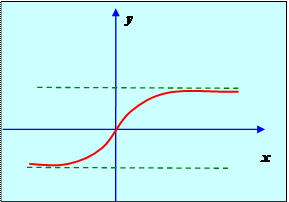
Рис. 6
3. Наклонные асимптоты – прямые вида y = kx + b. Найдем k и b. Поскольку
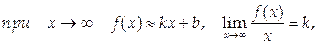
если этот предел существует, конечен и не равен нулю. Однако даже при выполнении этих условий наклонная асимптота может не существовать. Для ее существования требуется, чтобы имелся конечный предел при 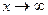 разности f(x) – kx. Этот предел будет равен b, так как
разности f(x) – kx. Этот предел будет равен b, так как
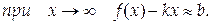
Замечание. Число вертикальных асимптот графика функции не ограничено, а наклонных и горизонтальных в сумме может быть не более двух (при 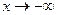 и при
и при 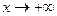 ).
).
 2015-07-14
2015-07-14 3916
3916








