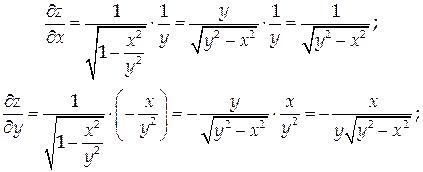
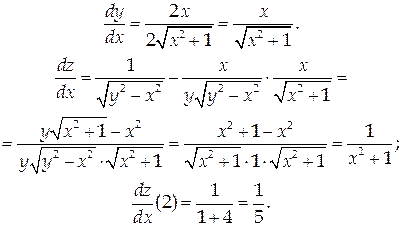
Ответ: 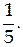
2.1.3. Неявные функции. Производные высших порядков
| Функция у от х, определяемая уравнением F (x, y) = 0, называется неявной функцией. |
Конечно, далеко не каждое уравнение подобного вида определяет у как однозначную (и, тем более, непрерывную) функцию от х. Например, уравнение эллипса
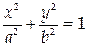
задает у как двузначную функцию от х:
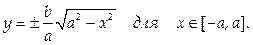
Условия существования однозначной и непрерывной неявной функции определяются следующей теоремой:
Теорема 1 (без доказательства). Пусть:
1) функция F (x,y) определена и непрерывна в некотором прямоугольнике
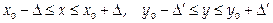
с центром в точке (х0, у0);
2) F (x0, y0) = 0;
3) при постоянном х F (x,y) монотонно возрастает (или убывает) с возрастанием у.
Тогда
а) в некоторой окрестности точки (х0, у0) уравнение
F (x, y) = 0
определяет у как однозначную функцию от х: y = f(x);
б) при х = х0 эта функция принимает значение у0: f (x0) = y0 ;
в) функция f (x) непрерывна.
Найдем при выполнении указанных условий производную функции y = f (x) по х.
Теорема 2. Пусть функция у от х задается неявно уравнением
F (x, y) = 0,
где функция F (x,y) удовлетворяет условиям теоремы 1. Пусть, кроме того,
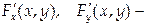
непрерывные функции в некоторой области D, содержащей точку (х,у), координаты которой удовлетворяют уравнению
F (x, y) = 0,
причем в этой точке
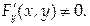
Тогда функция у от х имеет производную
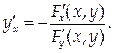
Доказательство.
Выберем некоторое значение х и соответствующее ему значение у. Зададим х приращение D х, тогда функция y = f (x) получит приращение D у. При этом F (x,y) = 0, F (x+ D x, y+ D y) = 0, поэтому F (x+ D x, y+ D y) – F (x,y) = 0. Слева в этом равенстве стоит полное приращение функции F (x,y), которое можно представить в виде:
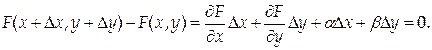
Разделив обе части полученного равенства на D х, выразим из него 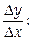
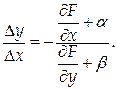
В пределе при 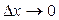 , учитывая, что
, учитывая, что
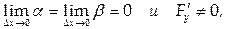
получим:
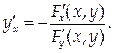
Теорема доказана.
Пример. Найдем 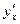 , если
, если
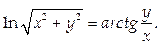
Найдем
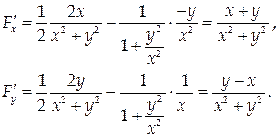
Тогда
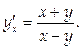
 2015-07-14
2015-07-14 322
322








