2015-07-14
348
Частные производные функции z = f (x,y) являются, в свою очередь,
функциями переменных х и у. Следовательно, можно найти их частные производные по этим переменным. Обозначим их так:
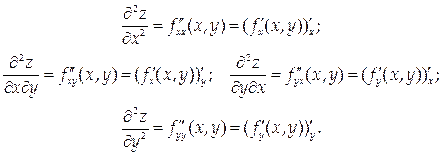
Таким образом, получены четыре частные производные 2-го порядка. Каждую из них можно вновь продифференцировать по х и по у и получить восемь частных производных 3-го порядка и т.д. Определим производные высших порядков так:
| Частной производной n -го порядкафункции нескольких переменных называется первая производная от производной (n – 1)-го порядка. |
Частные производные обладают важным свойством: результат дифференцирования не зависит от порядка дифференцирования (например,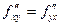 
). Докажем это утверждение.
Теорема 3. Если функция z = f (x,y) и ее частные производные
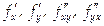
определены и непрерывны в точке М (х, у) и в некоторой ее окрестности, то в этой точке
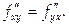
Доказательство.
Рассмотрим выражение
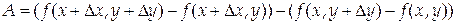
и введем вспомогательную функцию
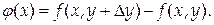
Тогда
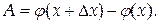
Из условия теоремы следует, что j (х) дифференцируема на отрезке [ x, x+ Δ x ], поэтому к ней можно применить теорему Лагранжа:
|
|
|
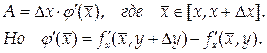
Так как в окрестности точки М определена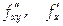 
дифференцируема на отрезке [ y, y + Δ y ], поэтому к полученной разности вновь можно применить теорему Лагранжа:
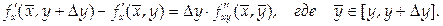
Тогда
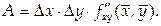
Изменим порядок слагаемых в выражении для А:
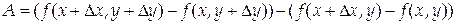
и введем другую вспомогательную функцию
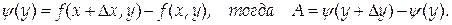
Проведя те же преобразования, что и для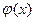 
, получим, что
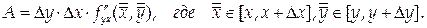
Следовательно,
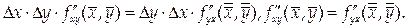
В силу непрерывност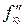и 
и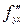 
.
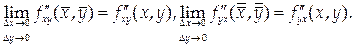Поэтому, переходя к пределу при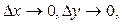 
получаем, что
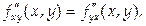
что и требовалось доказать.
Следствие. Указанное свойство справедливо для производных любого порядка и для функций от любого числа переменных.
