Чтобы вычислить производную функции y=f(x) в точке  , необходимо:
, необходимо:
1) вычислить значение функции в фиксированной точке  :
:
 ® f(
® f( ).
).
2) задать приращение аргумента 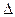 х; получить точку
х; получить точку  +
+  х, вычислить значение функции в ней:
х, вычислить значение функции в ней:
 +
+  х®f(
х®f( +
+  х);
х);
3) найти приращение функции:
 f=f(
f=f( +
+  х)-f(
х)-f( );
);
4) вычислить отношение:
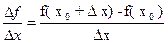 ;
;
5) найти предел полученного отношения при  х®0:
х®0:
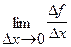 =
= 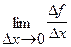 =
= 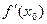 .
.
Пример:
7.1 Производная постоянной.
Пусть f(x)=C, c=const. Найти 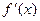 .
.
Решение.
1) Фиксируем  ; вычисляем значение функции в этой точке:
; вычисляем значение функции в этой точке:
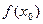 = С;
= С;  ®С;
®С;
2) задаем приращение аргумента  х, получаем точку
х, получаем точку  +
+  х, вычисляем значение функции в ней:
х, вычисляем значение функции в ней:
 +
+  х® f(
х® f( +
+  х)=С;
х)=С;
3) находим приращение функции:
 f = f(
f = f( +
+  х)- f(
х)- f( )=С-С=0;
)=С-С=0;
4) вычисляем отношение:
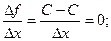
5) находим предел:
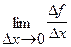 =
= 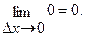
Итак, 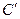 =0.
=0.
7.2 Производная линейной функции.
Пусть f(x)=kx+b; к, b – постоянные. Найдем 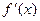 .
.
Решение.
Без комментариев проведем дифференцирование по шагам 1-5:
1)  ® f(
® f( )=k
)=k  +b;
+b;
2)  +
+  х®f(
х®f( +
+  х)=k(
х)=k( +
+  х)+b;
х)+b;
3)  f=f(
f=f( +
+  х)-f(
х)-f( )=k(
)=k( +
+  х)+b-(k
х)+b-(k  +b)= k
+b)= k  +k
+k  х-k
х-k  =k
=k  х;
х;
4) 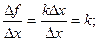
5) 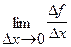 =
= 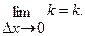
Итак, 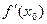 =k; т. к.
=k; т. к.  - фиксированная, но произвольная точка, то получим для любого х:
- фиксированная, но произвольная точка, то получим для любого х:
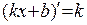 .
.
Упражнение:
7.3 Найти производные функций по определению.
а) f(x)= 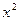 ; б) h(x)=
; б) h(x)= 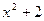 ; в)
; в) 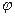 (x)=
(x)= 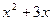 ; г)p(x)=
; г)p(x)= 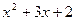 .
.
 2015-07-14
2015-07-14 983
983








