Пусть функция y = f(x) задана на интервале (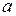 ;b).
;b).
Зафиксируем некоторую точку 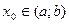 и вычислим значение функции в ней, получим f(
и вычислим значение функции в ней, получим f( ). Дадим
). Дадим  приращение
приращение 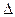 х
х 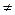 0, получим другую точку
0, получим другую точку  +
+  х
х 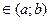 , вычислим значение функции в этой точке: f(
, вычислим значение функции в этой точке: f( +
+ 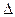 х). Вообще говоря, f(
х). Вообще говоря, f( +
+ 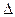 х)
х) 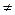 f(
f( ). Разность f(
). Разность f( +
+ 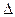 х) - f(
х) - f( ) называется приращением функции и обозначается
) называется приращением функции и обозначается 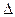 f=
f= 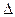 y.
y.
Определение. Производной 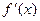 функции f(x) в точке
функции f(x) в точке  называется предел отношения приращения функции к вызвавшему его приращению аргумента, если последнее стремится к нулю, а предел существует и конечен:
называется предел отношения приращения функции к вызвавшему его приращению аргумента, если последнее стремится к нулю, а предел существует и конечен:
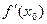 =
= 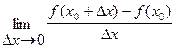 =
= 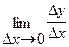 .
.
Производная обозначается 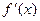 ;
; 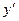 ;
; 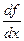 (читается: «эф штрих от х»; «у штрих»; «де эф по де икс»).
(читается: «эф штрих от х»; «у штрих»; «де эф по де икс»).
Функция, имеющая производную в точке, называется дифференцируемой в этой точке.
Операция нахождения производной от данной функции называется дифференцированием.
Функция f(x), х 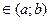 , имеющая производную в каждой точке этого интервала, называется дифференцируемой на этом интервале.
, имеющая производную в каждой точке этого интервала, называется дифференцируемой на этом интервале.
Можно доказать: если функция дифференцируема в некоторой точке, то она непрерывна в этой точке.
Обратное неверно: существуют функции, непрерывные в точке, но не имеющие производную в ней.
В задачах имеем:
1) Мгновенная скорость V(t) в момент 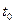 есть производная пути по времени:
есть производная пути по времени:
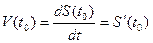 .
.
2) Мгновенная производительность труда z(t) в момент 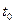 есть производная от количества произведенной продукции по времени:
есть производная от количества произведенной продукции по времени:
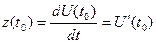 .
.
 2015-07-14
2015-07-14 1765
1765
