2015-07-14
2360
Производная и ее применение
Задача 1. (О мгновенной скорости) Прямолинейное движение материальной точки М совершается по закону S=S(t), где S – путь, пройденный точкой за время t от начала движения (рис. 3.1.) Найти скорость точки в момент t=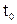 
.
S=S (t)
0 
M t
S=S (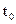
)
Рис. 7.1. Прямолинейное движение точки.
Решение. Каждому моменту времени соответствует определенный путь S, пройденный точкой М от точки 0 за время t. Путь есть функция времени: S = S(t). Для характеристики неравномерного движения используется понятие средней скорости. Если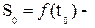 
, 
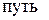
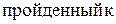
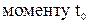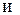
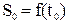
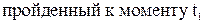,то средней скоростью за промежуток времени от 
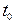до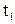 
называется число
.
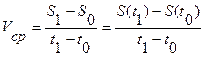Средняя скорость тем полнее характеризует движение, чем меньше длина промежутка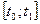 
.
Предел средней скорости за промежуток времени от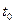 
до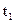 
при t, стремящемся к 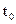, называется мгновенной скоростью V(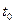) в момент :
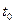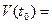
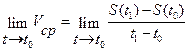, (7.1)
если этот предел существует и конечен.
Пример:
Лифт после включения движется по закону S(t) = 1,5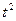 
+2t+12, где S – путь (в метрах), t – время (в секундах). Найти мгновенную скорость в момент времени .
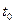Решение. По определению (3.1.) мгновенной скорости получаем:
=
= 
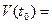
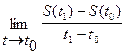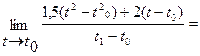
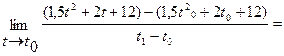
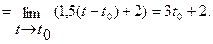
Следовательно, лифт после включения движется со скоростью V(t)=3t+2; через 15 секунд, мгновенная скорость будет составлять V(15)=3×15+2=47(м/с).
Задача 2. (О производительности труда) Количество произведенной продукции U за время t можно выразить функцией U=U(t). Найдем производительность труда в момент .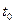
Решение. Если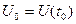 
- количество продукции, произведенной к моменту , 
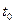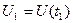- к моменту 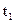, то средней производительностью труда за промежуток времени от 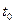до 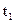называется число:
.
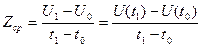Предел средней производительности труда за время 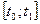при t, стремящемся к 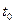, называется производительностью труда в момент времени :
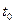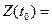
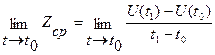(7.2)
если этот предел существует и конечен.
