I. Производная суммы функций.
Производная суммы двух дифференцируемых функций равна сумме производных этих функций:
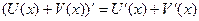 .
.
Доказательство. Рассмотрим две дифференцируемые в точке  функции
функции 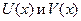 . Найдем производную функции f(x)=
. Найдем производную функции f(x)= 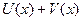 в точке
в точке  по шагам 1-5:
по шагам 1-5:
1)  ® f(
® f( )=
)= 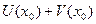 ;
;
2)  +
+  х®f(
х®f( +
+  х)=U(
х)=U( +
+  х)+V(
х)+V( +
+  х);
х);
3)  f=f(
f=f( +
+  х)-f(
х)-f( )=U(
)=U( +
+  х)+V(
х)+V( +
+ 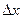 )-(U(
)-(U( )+V(
)+V( ))=(U(
))=(U( +
+  х)-U(
х)-U( ))+(V(
))+(V( +
+  х)-V(
х)-V( ))=
))=  U+
U+  V;
V;
4) 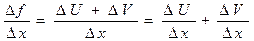 ;
;
5) 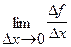 =
= 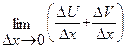 =
= 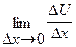 +
+ 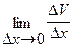 =
= 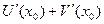 .
.
Итак, 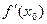 =
= 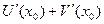 .
.
Аналогично для произвольной точки х из области дифференцируемости функций 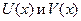 имеем:
имеем:
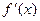 =
= 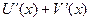 (7.3)
(7.3)
Задания: 1) Дайте словесный комментарий каждого шага 1-5; 2) почему возможны равенства в п. 5?
II. Производная произведения дифференцируемых функций вычисляется по формуле.
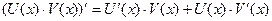 (7.4)
(7.4)
Следствие:
Постоянный множитель можно вынести за знак производной:
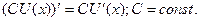
III. Производная частного двух дифференцируемых функций вычисляется по формуле:
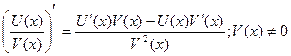 (7.5)
(7.5)
Формулы (7.4.), (7.5.) доказываются аналогично (7.3.)
Упражнение:
7.4 Используя правила вычисления производной, найдите производные следующих функций:
а) f(x)= 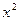 ; б) h(x)=
; б) h(x)= 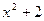 ; в)
; в) 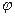 (x)=
(x)= 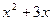 ; г) p(x)=
; г) p(x)= 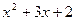 .
.
Сравните метод решения с использованным в упражнении 3.1.
7.5 Найти производные функций:
а) 2х;
б) 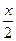 ;
;
в) 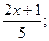
г) (х+1)(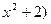 ;
;
в) (х+1)(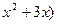 ;
;
г) 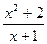 ;
;
д) 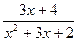 .
.
 2015-07-14
2015-07-14 670
670








