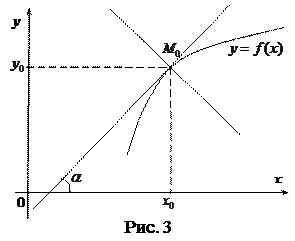 Рассмотрим кривую
Рассмотрим кривую 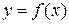 (рис. 3). Возьмем на этой кривой точку
(рис. 3). Возьмем на этой кривой точку 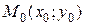 . Запишем уравнение касательной к кривой в этой точке, предполагая, что касательная не параллельна ось ординат. Зная геометрический смысл производной, отметим, что угловой коэффициент касательной равен значению производной в точке касания:
. Запишем уравнение касательной к кривой в этой точке, предполагая, что касательная не параллельна ось ординат. Зная геометрический смысл производной, отметим, что угловой коэффициент касательной равен значению производной в точке касания: 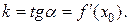
Поэтому уравнение касательной, проходящей через точку 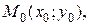 имеет вид:
имеет вид:
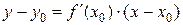 (14)
(14)
Прямая, проходящая через данную точку, перпендикулярно к касательной в этой точке, называется нормалью к кривой в данной точке.
Из определения нормали следует, что её угловой коэффициент 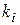 связан с угловым коэффициентом касательной
связан с угловым коэффициентом касательной 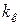 соотношением:
соотношением:
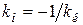 (15)
(15)
Следовательно, уравнение нормали к кривой 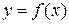 в точке
в точке 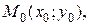 имеет вид:
имеет вид:
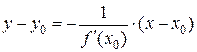 (16)
(16)
П р и м е р 13. Написать уравнения касательной и нормали к кривой а) 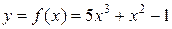 в точке
в точке 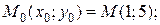 б)
б) 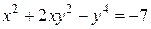 в точке
в точке 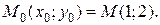
Решение.
а) Найдем производную функции: 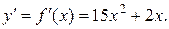 Угловой коэффициент касательной к кривой равен
Угловой коэффициент касательной к кривой равен 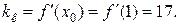 Следовательно, уравнение касательной (формула 14) имеет вид:
Следовательно, уравнение касательной (формула 14) имеет вид: 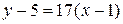 или
или 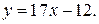 Угловой коэффициент нормали к кривой равен:
Угловой коэффициент нормали к кривой равен: 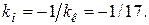 Следовательно, уравнение нормали (формула 16) имеет вид:
Следовательно, уравнение нормали (формула 16) имеет вид: 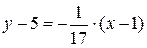 или
или 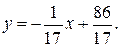
б) Из уравнения кривой найдем производную: 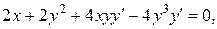 т.е.
т.е. 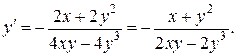 Следовательно,
Следовательно, 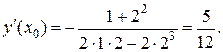 Тогда
Тогда 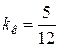 и уравнение касательной:
и уравнение касательной: 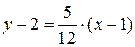 или
или 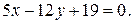 Тогда
Тогда 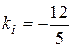 и уравнение нормали:
и уравнение нормали: 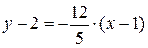 или
или 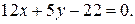
Варианты индивидуальных заданий для самостоятельной работы
З а д а н и е 1. Найти производную функции по определению.
| 1. | 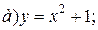 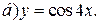 | 11. | 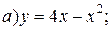 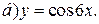 | 21. | 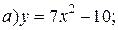 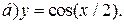 |
| 2. | а) 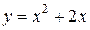 ; ; 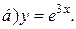 | 12. | а) 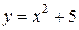 ; ; 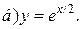 | 22. | а) 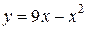 ; ; 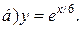 |
| 3. | а) 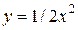 ; ; 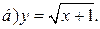 | 13. | а) 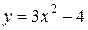 ; ; 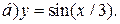 | 23. | а) 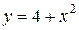 ; ; 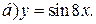 |
| 4. | а) 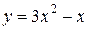 ; ; 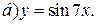 | 14. | а) 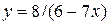 ; ; 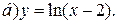 | 24. | а) 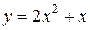 ; ; 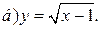 |
| 5. | а) 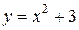 ; ; 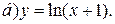 | 15. | а) 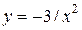 ; ; 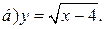 | 25. | а) 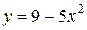 ; ; 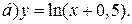 |
| 6. | 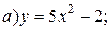 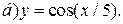 | 16. | а) 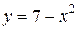 ; ; 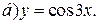 | 26. | 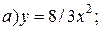 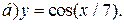 |
| 7. | а) 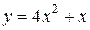 ; ; 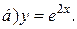 | 17. | а) 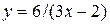 ; ; 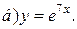 | 27. | а) 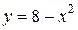 ; ; 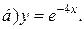 |
| 8. | а) 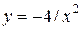 ; ; 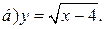 | 18. | а) 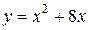 ; ; 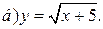 | 28. | а) 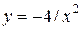 ; ; 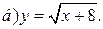 |
| 9. | а) 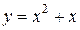 ; ; 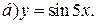 | 19. | а) 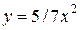 ; ; 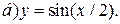 | 29. | а) 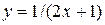 ; ; 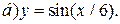 |
| 10. | а) 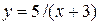 ; ; 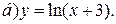 | 20. | а) 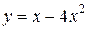 ; ; 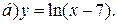 | 30. | а) 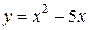 ; ; 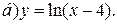 |
З а д а н и е 2. Вычислить производную функции пользуясь таблицей производных и правилами дифференцирования.
| 1. | 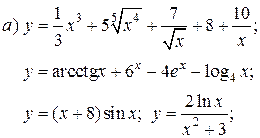 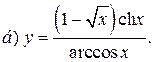 | 16. | 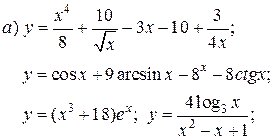 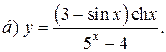 |
| 2. | 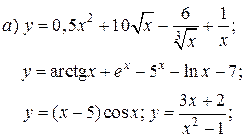 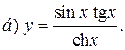 | 17. | 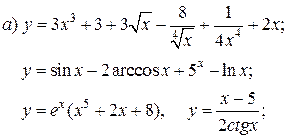 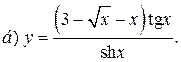 |
| 3. | 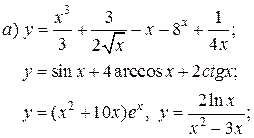 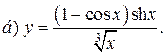 | 18. | 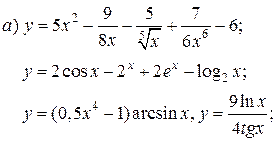 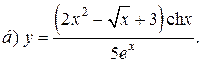 |
| 4. | 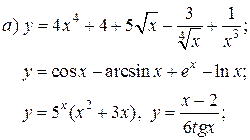 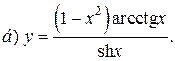 | 19. | 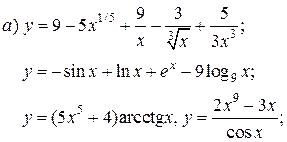 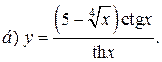 |
| 5. | 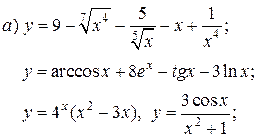 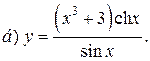 | 20. | 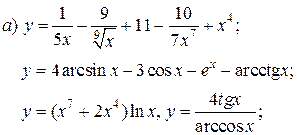 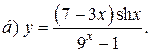 |
| 6. | 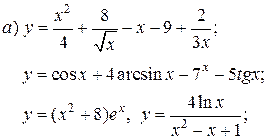 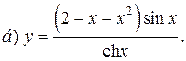 | 21. | 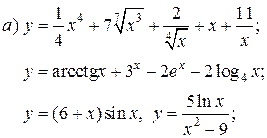 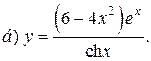 |
| 7. | 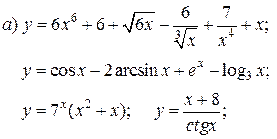 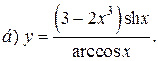 | 22. | 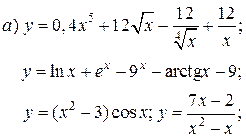 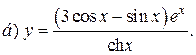 |
| 8. | 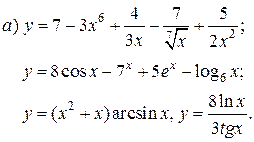 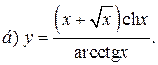 | 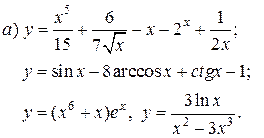 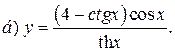 | |
| 9. | 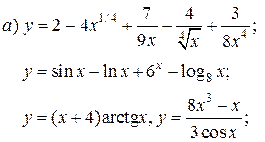 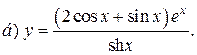 | 24. | 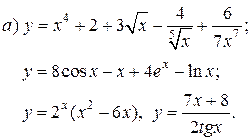 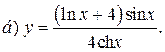 |
| 10. | 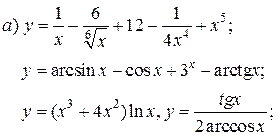 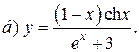 | 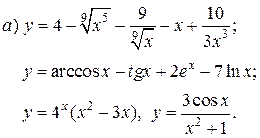 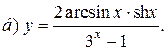 | |
| 11. | 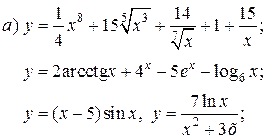 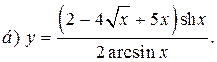 | 26. | 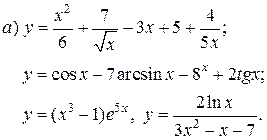 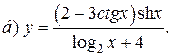 |
| 12. | 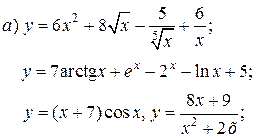 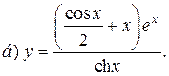 | 27. | 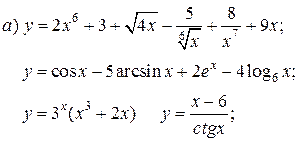 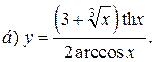 |
| 13. | 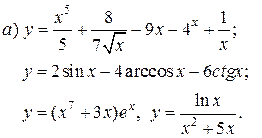 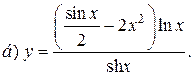 | 28. | 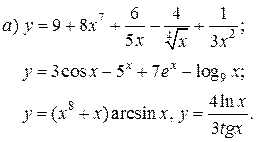 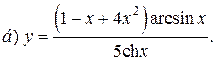 |
| 14. | 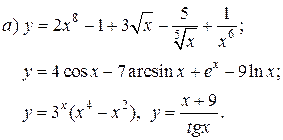 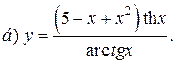 | 29. | 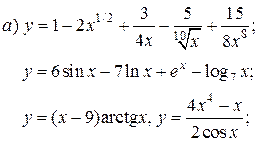 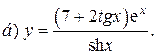 |
| 15. | 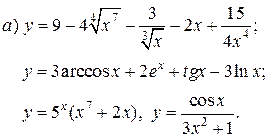 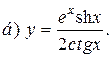 | 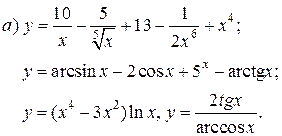 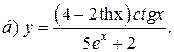 |
З а д а н и е 3. Вычислить производную сложной функции.
| 1. | 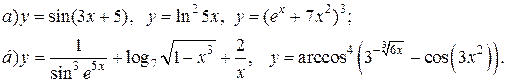 |
| 2. | 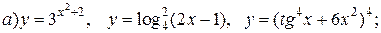 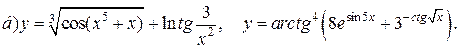 |
| 3. | 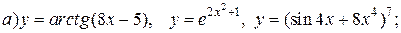 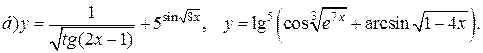 |
| 4. | 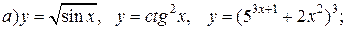 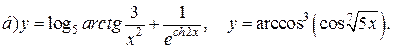 |
| 5. | 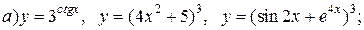 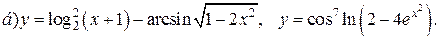 |
| 6. | 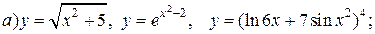 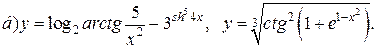 |
| 7. | 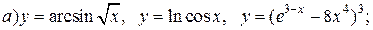 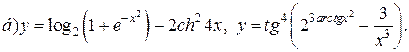 |
| 8. | 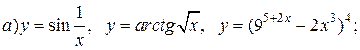 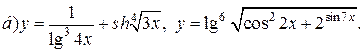 |
| 9. | 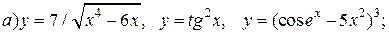 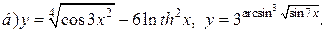 |
| 10. | 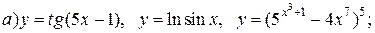 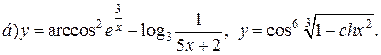 |
| 11. | 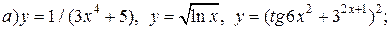 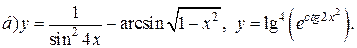 |
| 12. | 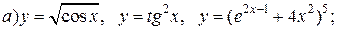 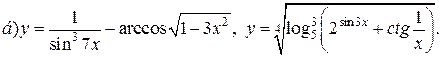 |
| 13. | 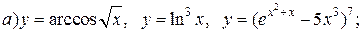 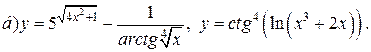 |
| 14. | 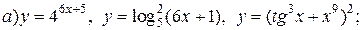 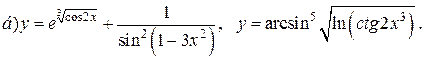 |
| 15. | 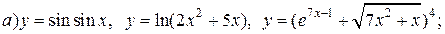 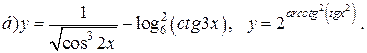 |
| 16. | 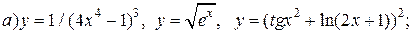 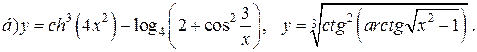 |
| 17. | 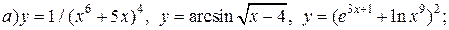 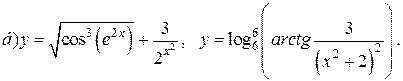 |
| 18. | 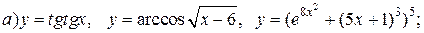 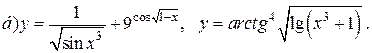 |
| 19. | 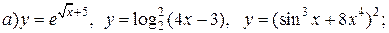 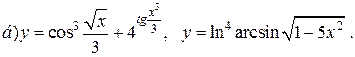 |
| 20. | 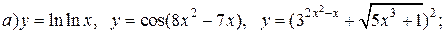 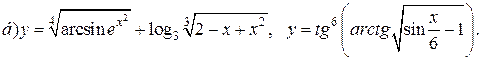 |
| 21. | 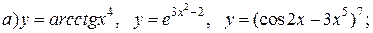 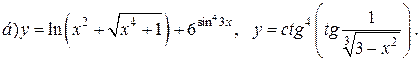 |
| 22. | 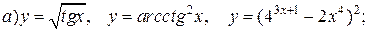 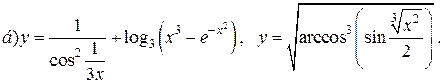 |
| 23. | 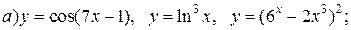 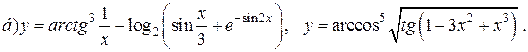 |
| 24. | 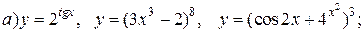 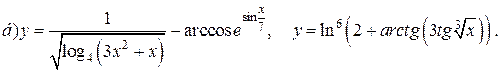 |
| 25. | 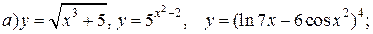 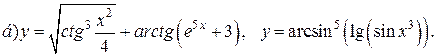 |
| 26. | 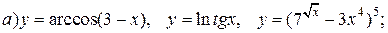 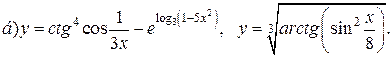 |
| 27. | 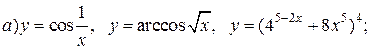 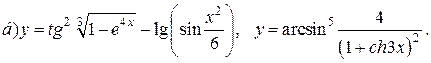 |
| 28. | 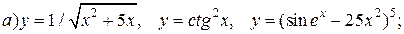 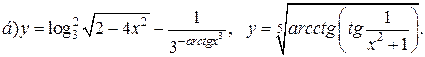 |
| 29. | 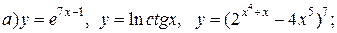 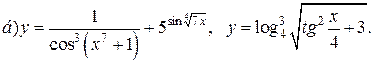 |
| 30. | 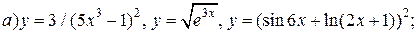 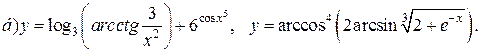 |
З а д а н и е 4. Найти производную функции, используя логарифмическую производную.
| 1. | 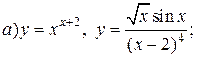 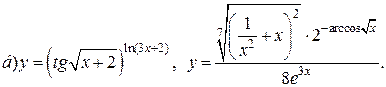 |
| 2. | 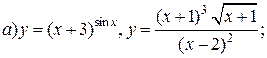 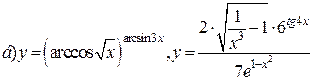 . . |
| 3. | 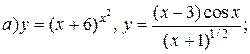 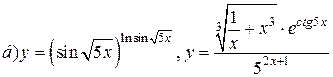 . . |
| 4. | 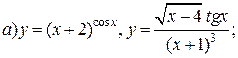 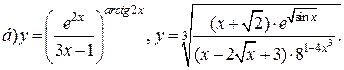 |
| 5. | 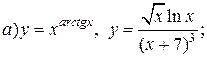 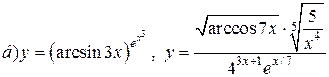 . . |
| 6. | 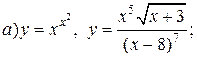 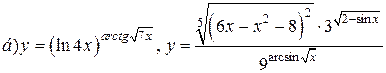 . . |
| 7. | 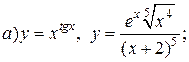 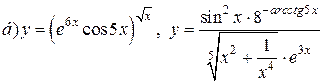 . . |
| 8. | 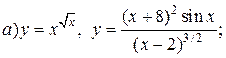 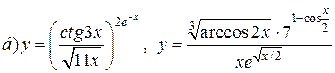 . . |
| 9. | 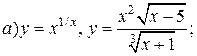 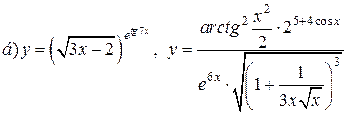 . . |
| 10. | 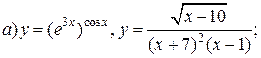 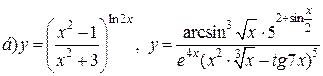 . . |
| 11. | 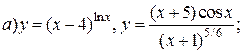 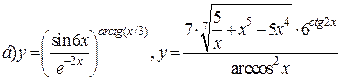 . . |
| 12. | 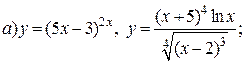 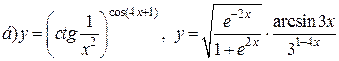 . . |
| 13. | 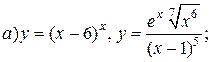 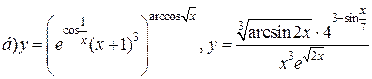 . . |
| 14. | 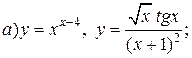 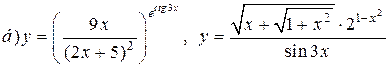 . . |
| 15. | 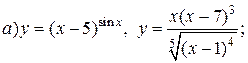 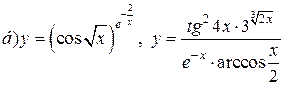 . . |
| 16. | 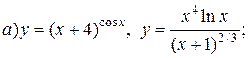 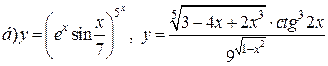 . . |
| 17. | 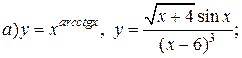 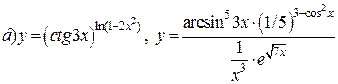 . . |
| 18. | 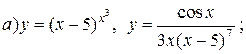 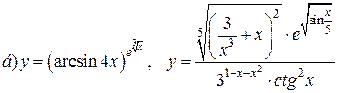 . . |
| 19. | 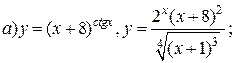 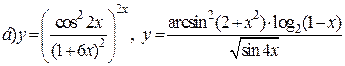 . . |
| 20. | 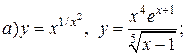 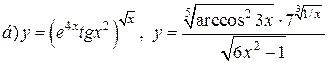 . . |
| 21. | 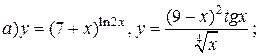 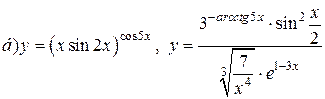 . . |
| 22. | 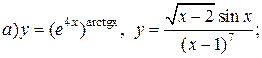 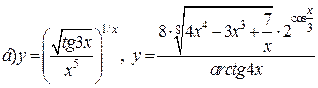 . . |
| 23. | 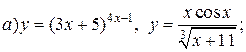 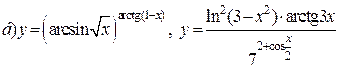 . . |
| 24. | 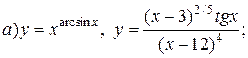 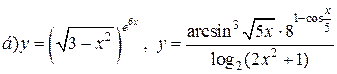 . . |
| 25. | 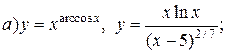 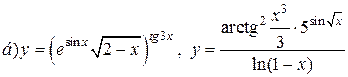 . . |
| 26. | 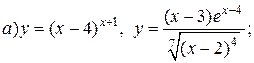 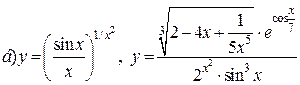 . . |
| 27. | 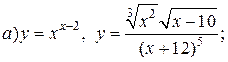 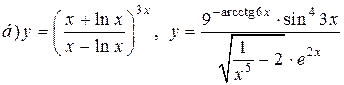 . . |
| 28. | 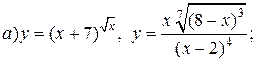 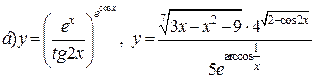 . . |
| 29. | 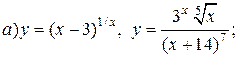 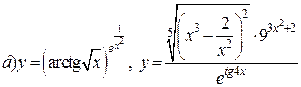 . . |
| 30. | 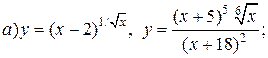 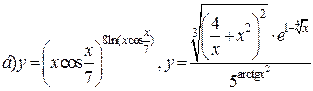 . . |
З а д а н и е 5. Найти производную неявно заданной функции.
| 1. | а) 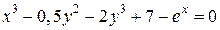 ; б) ; б) 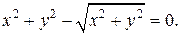 | 16. | а) 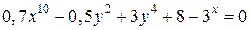 ; б) ; б) 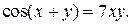 |
| 2. | а) 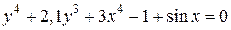 ; б) ; б) 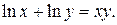 | 17. | а) 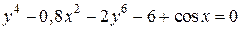 ; б) ; б) 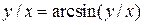 . . |
| 3. | а) 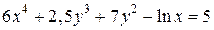 ; б) ; б) 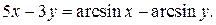 | 18. | а) 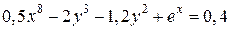 ; б) ; б) 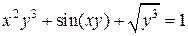 . . |
| 4. | а) 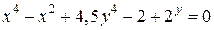 ; б) ; б) 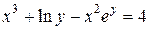 . . | 19. | а) 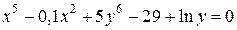 ; б) ; б) 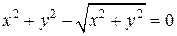 . . |
| 5. | а) 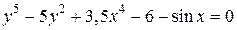 ; б) ; б) 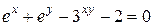 . . | 20. | а) 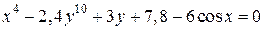 ; б) ; б) 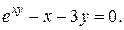 |
| 6. | а) 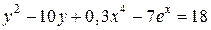 ; б) ; б) 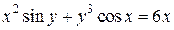 . . | 21. | а) 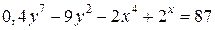 ; б) ; б) 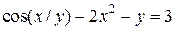 . . |
| 7. | а) 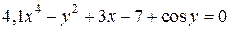 ; б) ; б) 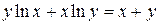 . . | 22. | а) 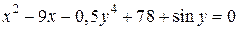 ; б) ; б) 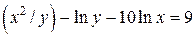 . . |
| 8. | а) 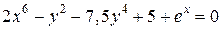 ; б) ; б) 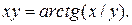 | 23. | а) 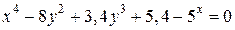 ; б) ; б) 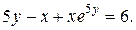 |
| 9. | а) 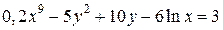 ; б) ; б) 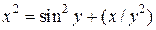 . . | 24. | а) 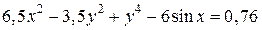 ; б) ; б) 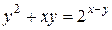 . . |
| 10. | а) 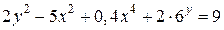 ; б) ; б) 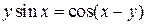 . . | 25. | а) 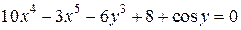 ; б) ; б) 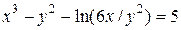 . . |
| 11. | а) 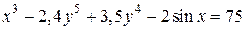 ; б) ; б) 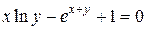 . . | 26. | а) 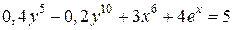 ; б) ; б) 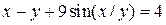 . . |
| 12. | а) 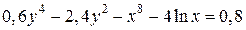 ; б) ; б) 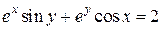 . . | 27. | а) 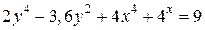 ; б) ; б) 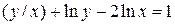 . . |
| 13. | а) 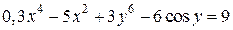 ; б) ; б) 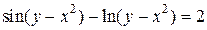 . . | 28. | а) 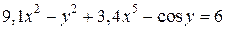 ; б) ; б)  . . |
| 14. | а) 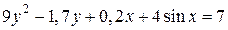 ; б) ; б) 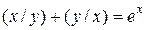 . . | 29. | а) 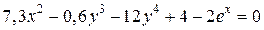 ; б) ; б) 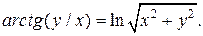 |
| 15. | а) 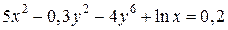 ; б) ; б) 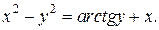 | 30. | а) 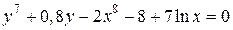 ; б) ; б) 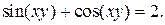 |
З а д а н и е 6. Найти производные 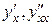 функций, заданных в параметрическом виде.
функций, заданных в параметрическом виде.
| 1. | а) 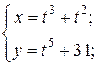 б) б) 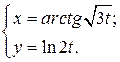 | 16. | а) 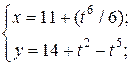 б) б) 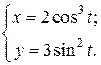 |
| 2. | а) 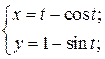 б) б) 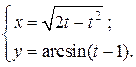 | 17. | а) 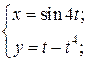 б) б) 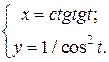 |
| 3. | а) 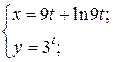 б) б) 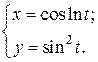 | 18. | а) 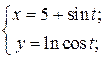 б) б) 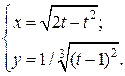 |
| 4. | а) 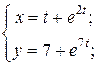 б) б) 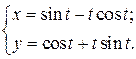 | 19. | а) 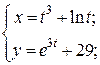 б) б) 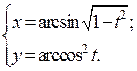 |
| 5. | а) 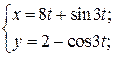 б) б) 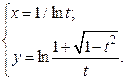 | 20. | а) 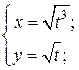 б) б) 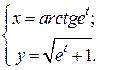 |
| 6. | а) 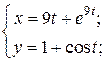 б) б) 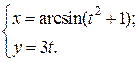 | 21. | а) 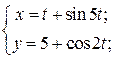 б) б) 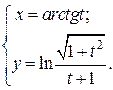 |
| 7. | а) 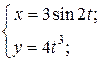 б) б) 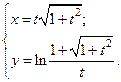 | 22. | а) 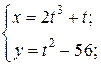 б) б) 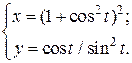 |
| 8. | а) 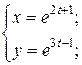 б) б) 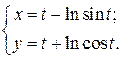 | 23. | а) 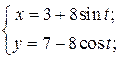 б) б) 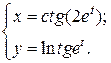 |
| 9. | а) 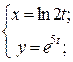 б) б) 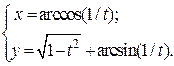 | 24. | а) 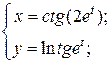 б) б) 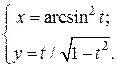 |
| 10. | а) 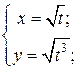 б) б) 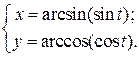 | 25. | а) 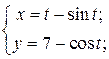 б) б) 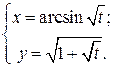 |
| 11. | а) 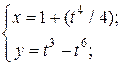 б) б) 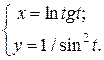 | 26. | а) 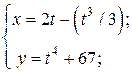 б) б) 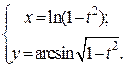 |
| 12. | а) 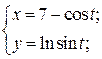 б) б) 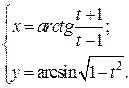 | 27. | а) 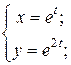 б) б) 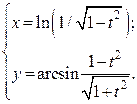 |
| 13. | а) 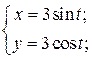 б) б) 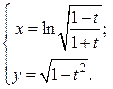 | 28. | а) 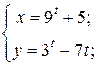 б) б) 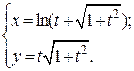 |
| 14. | а) 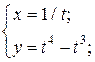 б) б) 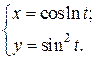 | 29. | а) 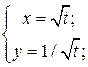 б) б)  |
| 15. | а) 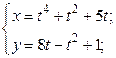 б) б) 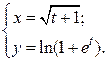 | 30. | а) 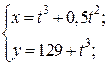 б) б) 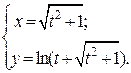 |
З а д а н и е 7. Найти производную второго порядка
| 1. | а) 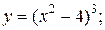 б) б) 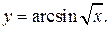 | 16. | а) 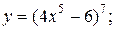 б) б) 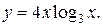 |
| 2. | а) 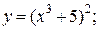 б) б) 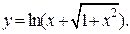 | 17. | а) 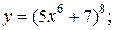 б) б) 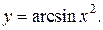 |
| 3. | а) 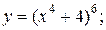 б) б) 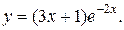 | 18. | а) 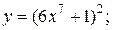 б) б) 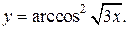 |
| 4. | а) 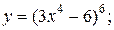 б) б) 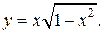 | 19. | а) 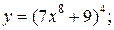 б) б) 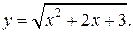 |
| 5. | а) 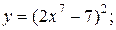 б) б) 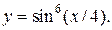 | 20. | а) 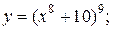 б) б) 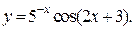 |
| 6. | а) 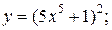 б) б) 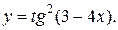 | 21. | а) 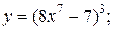 б) б) 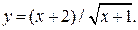 |
| 7. | а) 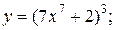 б) б) 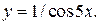 | 22. | а) 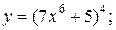 б) б) 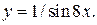 |
| 8. | а) 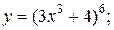 б) б) 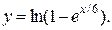 | 23. | а) 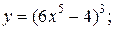 б) б) 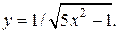 |
| 9. | а) 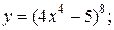 б) б) 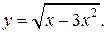 | 24. | а) 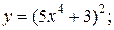 б) б) 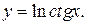 |
| 10. | а) 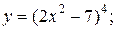 б) б) 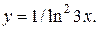 | 25. | а) 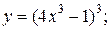 б) б) 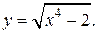 |
| 11. | а) 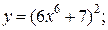 б) б) 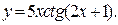 | 26. | а) 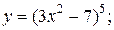 б) б) 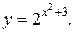 |
| 12. | а) 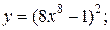 б) б) 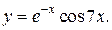 | 27. | а) 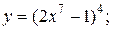 б) б) 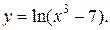 |
| 13. | а) 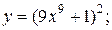 б) б) 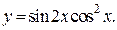 | 28. | а) 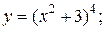 б) б) 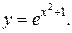 |
| 14. | а) 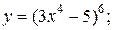 б) б) 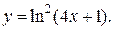 | 29. | а) 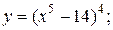 б) б) 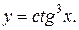 |
| 15. | а) 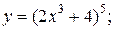 б) б) 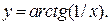 | 30. | а) 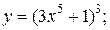 б) б) 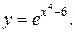 |
З а д а н и е 8. Записать дифференциал функции.
| 1. | 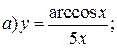 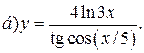 | 16. | 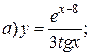 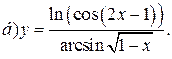 |
| 2. | 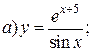 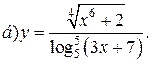 | 17. | 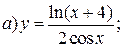 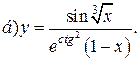 |
| 3. | 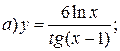 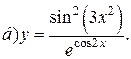 | 18. | 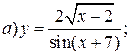 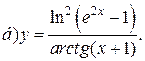 |
| 4. | 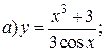 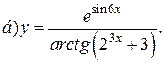 | 19. | 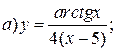 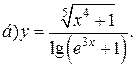 |
| 5. | 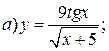 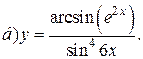 | 20. | 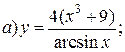 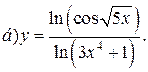 |
| 6. | 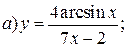 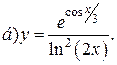 | 21. | 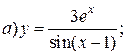 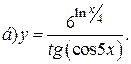 |
| 7. | 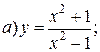 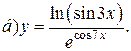 | 22. | 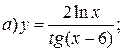 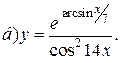 |
| 8. | 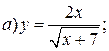 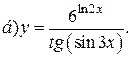 | 23. | 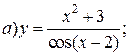 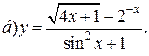 |
| 9. | 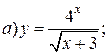  | 24. | 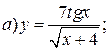 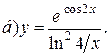 |
| 10. | 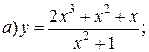 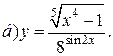 | 25. | 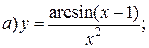 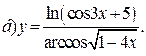 |
| 11. | 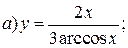 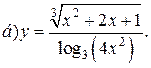 | 26. | 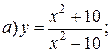 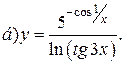 |
| 12. | 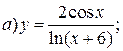 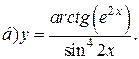 | 27. | 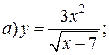 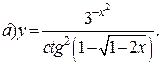 |
| 13. | 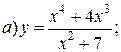 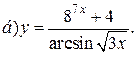 | 28. | 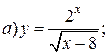 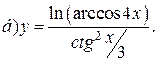 |
| 14. | 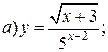 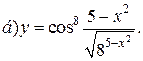 | 29. | 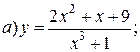 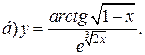 |
| 15. | 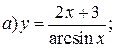 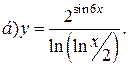 | 30. | 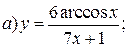 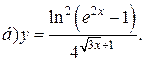 |
З а д а н и е 9. Записать уравнения касательной и нормали к кривой в точке 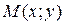 .
.
| 1. | а) 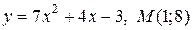 ; б) ; б) 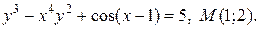 | |
| 2. | а) 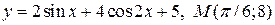 ; б) ; б) 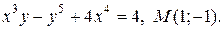 | |
| 3. | а) 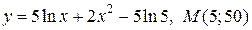 ; б) ; б) 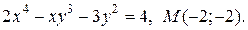 | |
| 4. | а) 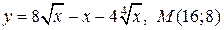 ; б) ; б)  | |
| 5. | а) 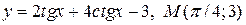 ; б) ; б) 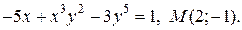 | |
| 6. | а) 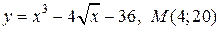 ; б) ; б) 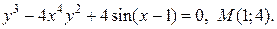 | |
| 7. | а) 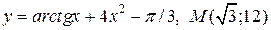 ; б) ; б) 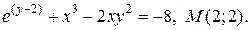 | |
| 8. | а) 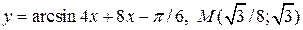 ; б) ; б) 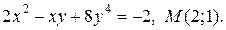 | |
| 9. | а) 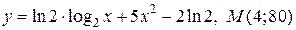 ; б) ; б) 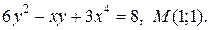 | |
| 10. | а) 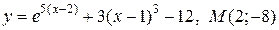 ; б) ; б) 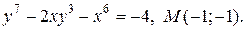 | |
| 11. | а) 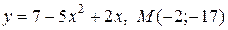 ; б) ; б) 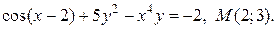 | |
| 12. | а) 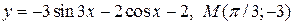 ; б) ; б) 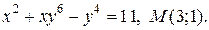 | |
| 13. | а) 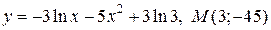 ; б) ; б) 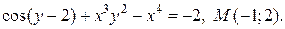 | |
| 14. | а) 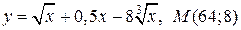 ; б) ; б) 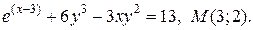 | |
| 15. | а) 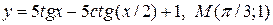 ; б) ; б) 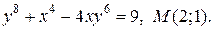 | |
| 16. | а) 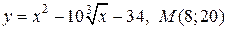 ; б) ; б) 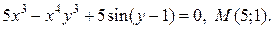 | |
| 17. | а) 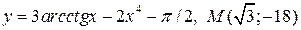 ; б) ; б) 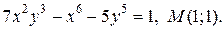 | |
| 18. | а) 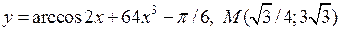 ; б) ; б)
Подборка статей по вашей теме:
|
 2015-07-14
2015-07-14 1758
1758
