Касательная к графику функции

Пусть М, М₀ – две различные точки кривой (рис. 7.2)

T М´

М₀ М L

Рис. 7.2. Касательная к кривой

Прямая (ММ₀) называется секущей кривой L.

Пусть точка М, перемещаясь по кривой L, приближается к точке М₀. Если секущая стремится занять предельное положение (М₀Т), то прямая (ТМ₀) называется касательной к кривой L в точке М₀.

Допустим, кривая L является графиком непрерывной функции y=ƒ(x) (рис. 3.3).

y

M(x;y)

y₀

M₀(x₀;y₀)

β α

0 х₀ x x

На рис. 7.3: если (М₀М) – секущая, 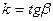- угловой коэффициент секущей, тогда

; .

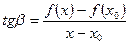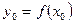Пусть х стремится к х₀, тогда точка М стремится по кривой L к М₀. Если функция ƒ(х) имеет производную в точке х₀, то

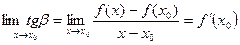
Таким образом, производная функции ƒ(х) в точке х₀ равна угловому коэффициенту касательной к графику функции в точке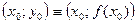

Уравнение прямой с угловым коэффициентом 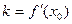имеет вид:

y = kx+b или y=ƒ’(х₀)∙x+b.

Для вычисления воспользуемся тем, что касательная проходит через точку М₀. Подставляем координаты точки М₀ (х₀ ;ƒ(х₀)) в уравнение касательной:

ƒ(х₀) = ƒ′(х₀)∙х₀+b,

откуда

b = ƒ(х₀)- ƒ′(х₀)∙ х₀

Уравнение касательной принимает вид:

y =ƒ′(х₀)∙(x- х₀)+ƒ(х₀) (3.8)

Пример:

7.24 Написать уравнение касательной к параболе y=x² в точке с абсциссой х₀=1.

Решение: Имеем ƒ(х₀)=х²₀; ƒ(х₀)=1 при х₀=1; ƒ′(х₀)=2∙ х₀; ƒ′(х₀)=2 при х₀=1.

Уравнение касательной: y=2∙(x-1)+1 или y=2∙x-1.

Упражнения: Написать уравнения касательных к графику функции y=ƒ(x) в точке с абсциссой х₀:

7.25 а) y=x3; х₀=1;

б) 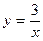; х₀=1;

в) 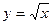; х₀=4

г) y=x²-2x+5; х₀ =0,5